Equivalent Resistance and Branch Currents in Non-simple Circuits

[BeRiemann]

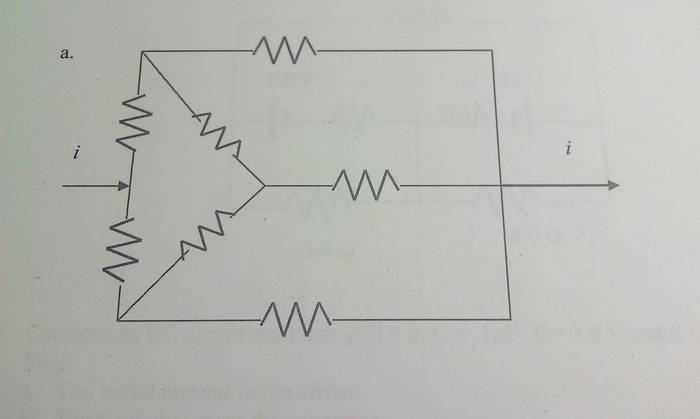
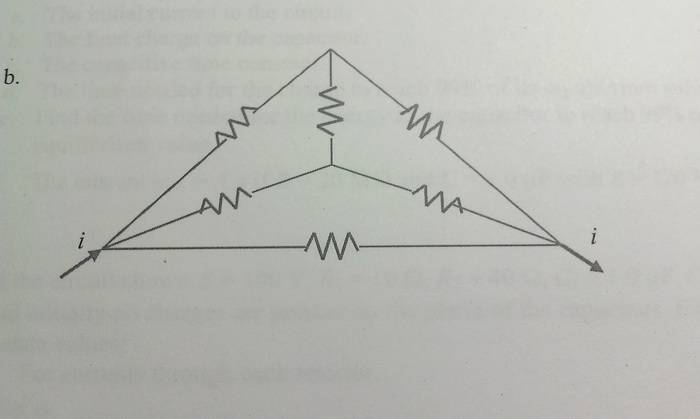
I'm asked to find an equivalent resistance and the current through each branch of the following circuits. (r is a fixed arbitrary value for all resistors in the circuits)

Homework Equations

V=IR
Sum of I at a node = 0
Sum of V about a closed loop = 0

The Attempt at a Solution

I've been playing with both KVL and KCL equations trying get a working answer, but none of my attempts seem to be anything but cyclically finding me zero. My problem is how I consider the input current. Is it right to make the assumption that I essentially have a battery there which has the value of ε = i*R_equivalent. The circuits cannot be broken down in terms of parallel or series from what I've seen.

 

[sandy.bridge]

Are you familiar with \Delta -Y conversions? I would start by implementing these conversions to determine equivalent resistances.

 

[gneill]

Sometimes symmetry offers opportunities for circuit simplification, particularly in 'contrived' circuits like these; the problems are designed to get you to think about and recognize these opportunities. Take the first circuit for example.

Yes, when you don't find obvious serial or parallel resistor combinations to exploit you could bring out bigger and better weapons like Δ-Y transformations or even mesh or nodal analysis. But you might also recognize the fact that there is a line of symmetry running through the circuit, where the top half is a mirror image of the bottom half. What does that do for you? It means that the currents in each of the "reflected" paths and components will be the same. It also means that image-pairs of nodes will have the same potential.

When two nodes always have the same potential they are essentially equivalent nodes. You could run a wire between those nodes and it would not affect circuit operation in any way. In effect then you can treat them as being the same node! When you do that, a number of new effective parallel connections appear.

Imagine folding the circuit along the line of symmetry. Any components that get overlaid with their mirror partner are now parallel pairs -- so replace them with half value resistors. Observe the new simplified circuit!

 

[BeRiemann]

I'm not familiar with delta-Y conversions, but I'll have to take a look at them if they're useful.
I was thinking along those same paths for symmetry, my biggest obstacle was just knowing if it was actually a valid technique. Thanks!