roughwinds
- 11
- 0
I'm trying to deduce the differential equation for temperature for a triangular fin:
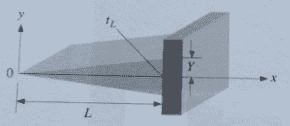
I know that for a rectangular fin, such as:
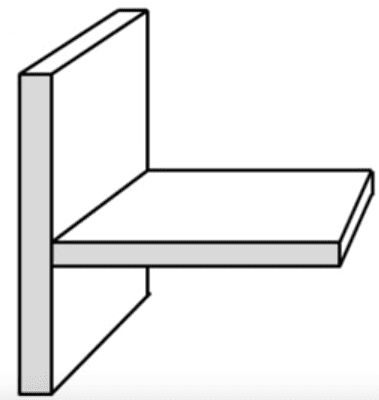
I can do:
Energy entering the left:
q_x= -kA\frac{dT(x)}{dx}
Energy leaving the right:
q_{x+dx} = -kA\frac{dT(x)}{dx} - kA\frac{d² T(x)}{dx²}dx
Energy lost by convection:
dq_{conv} = h_eA(T-T_e)
dq_{conv} = h_eP(T-T_e)dx
q_x - q_{x+dx} - dq_{conv} = 0
q_x = q_{x+dx} + dq_{conv}
-kA\frac{dT(x)}{dx} = -kA\frac{dT(x)}{dx} - kA\frac{d²T(x)}{dx²}dx + h_eP(T-T_e)dx
kA\frac{d²T(x)}{dx²}dx = h_eP(T-T_e)dx
\frac{d²T(x)}{dx²} = \frac{h_eP(T-T_e)}{kA}
But I don't understand why A = Pdx on the energy lost by convection, so I don't know how to adapt that for a triangular fin.
Seems to me that T(x,y,z) still changes predominantly on the x axis, so I assume the other two equations remain unchanged.
I know that for a rectangular fin, such as:
I can do:
Energy entering the left:
q_x= -kA\frac{dT(x)}{dx}
Energy leaving the right:
q_{x+dx} = -kA\frac{dT(x)}{dx} - kA\frac{d² T(x)}{dx²}dx
Energy lost by convection:
dq_{conv} = h_eA(T-T_e)
dq_{conv} = h_eP(T-T_e)dx
q_x - q_{x+dx} - dq_{conv} = 0
q_x = q_{x+dx} + dq_{conv}
-kA\frac{dT(x)}{dx} = -kA\frac{dT(x)}{dx} - kA\frac{d²T(x)}{dx²}dx + h_eP(T-T_e)dx
kA\frac{d²T(x)}{dx²}dx = h_eP(T-T_e)dx
\frac{d²T(x)}{dx²} = \frac{h_eP(T-T_e)}{kA}
But I don't understand why A = Pdx on the energy lost by convection, so I don't know how to adapt that for a triangular fin.
Seems to me that T(x,y,z) still changes predominantly on the x axis, so I assume the other two equations remain unchanged.