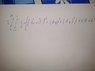Find average velocity of a sphere which expands and moves

[Quarlep]

Homework Statement

Find the average velocity of shell while its moves a velocity v' and expands a velocity v.
Sphere radius is R
Expansion velocity v
Movement velocity v'

Homework Equations

I think there's no need an equation.[/B]

The Attempt at a Solution

I try to find average velocity but its vector.So I made max velocity v+v' and min velocity v-v' then I add them and divide two and I find v but I think I made a mistake.

 

[Puma]

That's right. If you draw a line in any direction through the shell's centre those expansion velocities cancel out so you are just left with v

 

[Quarlep]

Expansion velocities can't cancel v is expansion velocity v' is object velocity.I didnt mention it but shell is a surface of sphere.And I didnt understand your prove

 

[Puma]

Ok ignore v' eg imagine the sphere is stationary what is the average velocity of the sphere shell. The speed is v but the velocity which is a vector cancels out: if you imagine any point on the sphere - there is one going in exactly the opposite direction so when you add them all up the answer is 0.

 

[Quarlep]

So that expansion velocities cancels and left only v which speed of sphere

 

[Quarlep]

I am so so sorry .I made a mistake in my equation it must be v'-v not v-v' my fault.
I want to ask another question.Before sphere moves, shell energy will be 1/2mv^2(v is shell expansion speed) but after sphere moves shell energy will be 1/2mv^2 (v is the sphere velocity) isn't it ?

 

[AlephNumbers]

So that expansion velocities cancels and left only v which speed of sphere

The expansion velocities don't "cancel out" unless we are considering the velocity of the center of mass of the sphere. In which case you are right, the velocity of the center of mass of the sphere should stay constant.

I want to ask another question.Before sphere moves, shell energy will be 1/2mv^2(v is shell expansion speed) but after sphere moves shell energy will be 1/2mv^2 (v is the sphere velocity) isn't it ?

No, I don't believe so. Energy is a scalar quantity, so the expansion velocities will not conveniently cancel out. The only way that I am able to come to any sort of meaningful conclusion regarding the kinetic energy of the sphere is by considering the kinetic energy of the sphere at the very instant that the sphere begins to expand. Here is a picture to help you visualize the situation.

 

[Quarlep]

I am not talking about kinetic energy of sphere.I am talking about shell energy

 

[AlephNumbers]

I am not talking about kinetic energy of sphere.I am talking about shell energy

Sorry, the shell. I accidentally used the term sphere instead of shell. Please forgive me.

shell energy will be 1/2mv^2(v is shell expansion speed) but after sphere moves shell energy will be 1/2mv^2 (v is the sphere velocity) isn't it ?

Can you explain your reasoning?

 

[Quarlep]

When shell is not moving shell energy will be the "energy " which that energy causes expension of shell and that's the 1/2m₂v².Then shell moves and the speed of shell will be (as you mentioned vectors of speeds which you add them and calculations shows a v which is the speed of movement) so energy of shell will be 1/2m_shellv² v is speed of sphere

 

[AlephNumbers]

When shell is not moving shell energy will be the "energy " which that energy causes expension of shell and that's the 1/2m₂v².Then shell moves and the speed of shell will be (as you mentioned vectors of speeds which you add them and calculations shows a v which is the speed of movement) so energy of shell will be 1/2m_shellv² v is speed of sphere

My good chap, I am afraid that any solution to your somewhat vague question is significantly more complicated. Why don't you examine the problem further, and maybe sleep on it. Then show us what you have come up with. Perhaps my diagram will give you some inspiration.

 

[Quarlep]

Look the prove of speed.

 

[haruspex]

Look the prove of speed.

Yes, that correctly shows the expansion cancels out when computing average velocity. But average KE is not given by squaring average velocity. You have to find the KE of each element separately and then integrate.
There's an analogous result in statistics: the variance is the mean square minus the square of the mean.

 

[Quarlep]

There's an analogous result in statistics: the variance is the mean square minus the square of the mean.

I didnt understand this and here what I found

 

[haruspex]

I didnt understand this and here what I found

The integrals on the left are ok, but they don't give the answer on the right. please post your steps.

 

[Quarlep]

Here the steps

 

[haruspex]

Here the steps

The integrals of sin² and cos² cannot cancel to zero. The integrands are non-negative everywhere.
You'll find it simpler if you collapse v²sin² + v² cos² to v².

 

[Quarlep]

they can cancel to zero.If we integrate (sinx)² between 0 and π we get π/2 then we integrate same thing again between π and 0 we get -π/2 there's nothing wrong look carefully.Only my first equation can be wrong.But you said that's true so we get mv²

 

[haruspex]

then we integrate same thing again between π and 0

There's your problem, you're running the integral backwards, getting a negative result from an integrand that's never negative.

 

[Quarlep]

You told me the right side of the equation is true.If its true then we need to integrate backward.If you think different way prove me using math.Or my first equation is wrong.

 

[haruspex]

You told me the right side of the equation is true.

Yes, I'm sorry, I didn't notice the reversed bounds on the second one.

 

[Quarlep]

Can you tell me right equation please.I couldn't figure it out myself that's way I asked in this forum.

 

[haruspex]

Can you tell me right equation please.I couldn't figure it out myself that's way I asked in this forum.

As I posted, the best is to simplify the expression first. sin²x+cos²x=1.
For the integral bounds, just put them in the order of increasing variable value, 0 to pi, or -pi to 0, not pi to 0.

Oh dear, I must be half asleep. I forgot this is about a spherical shell, not simply a circle. That means you should be using a double integral in spherical polar coordinates.

 

[AlephNumbers]

Oh dear, I must be half asleep. I forgot this is about a spherical shell, not simply a circle. That means you should be using a double integral in spherical polar coordinates.

Up past your bedtime doing double integrals, I see.

Perhaps we should assume a thin spherical shell in order to simplify this problem a little? I get the impression that finding the kinetic energy of this moving and expanding shell was not intended to be a part of this problem in the first place.

 

[Quarlep]

Yeah its a spherical shell.All equations should change now.Can somebody telll me the full equation please ( You need to write it) As I mentioned its not a circle its a sphere.I am 18 I learned Integrals 1 week ago.I don't how to do it myself Just please can somebody calculate it for me.Its very important please.

 

[Quarlep]

Here what I found.Is that works ?

 

[haruspex]

Yeah its a spherical shell.All equations should change now.Can somebody telll me the full equation please ( You need to write it) As I mentioned its not a circle its a sphere.I am 18 I learned Integrals 1 week ago.I don't how to do it myself Just please can somebody calculate it for me.Its very important please.

I wasn't sure whether you just needed a way to get an answer or wanted to see how it could all be done with integrals. Integrals can be avoided, pretty much. Just use the symmetry. Consider two diametrically opposite mass elements and add up their KEs.

 

[Quarlep]

I wasn't sure whether you just needed a way to get an answer or wanted to see how it could all be done with integrals. Integrals can be avoided, pretty much. Just use the symmetry. Consider two diametrically opposite mass elements and add up their KEs.

Its my project homeworks one part.So I need equations. Symmetry Idea is very good.I am thinking.You didnt mention anything about my eq but can it be true

 

[haruspex]

Its my project homeworks one part.So I need equations. Symmetry Idea is very good.I am thinking.You didnt mention anything about my eq but can it be true

I'm afraid I could not make any sense of your latest equations. There seem to some parentheses and plus signs missing, I couldn't understand the bit about "points for which... are constant", or how you would be integrating wrt r instead of wrt theta and phi.

 

[Quarlep]

I ll explain it in a moment but now I made a circle shell energy formula.