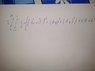- #31
Find average velocity of a sphere which expands and moves
- Thread starter Quarlep
- Start date
Click For Summary
SUMMARY
The discussion focuses on calculating the average velocity of a spherical shell that expands and moves, specifically addressing the velocities involved: expansion velocity (v) and movement velocity (v'). Participants clarify that while expansion velocities can cancel out in certain contexts, the average velocity remains dependent on the movement velocity v'. The kinetic energy of the shell is also discussed, emphasizing that energy is a scalar quantity and does not simply cancel out like vector quantities. The conversation highlights the need for proper mathematical treatment, including the use of double integrals in spherical coordinates for accurate calculations.
PREREQUISITES- Understanding of vector and scalar quantities in physics
- Familiarity with kinetic energy concepts and equations
- Knowledge of spherical coordinates and double integrals
- Basic principles of symmetry in physics problems
- Study the derivation of kinetic energy in spherical coordinates
- Learn about the application of double integrals in physics problems
- Explore the concept of center of mass and its implications in motion
- Review vector addition and cancellation in the context of physics
Students studying physics, particularly those focusing on mechanics and energy concepts, as well as educators looking for examples of complex motion and energy calculations involving spherical objects.
- #32
- 42,802
- 10,495
Yes, that's right for an expanding ring. A spherical shell is the same except that you need a double integral.Quarlep said:
Let me give you a start on that. Are you familiar with Archimedes' proof of the area of a sphere?
- #33
Quarlep
- 257
- 4
No
- #34
- 42,802
- 10,495
He effectively invented calculus. He considered a cylinder enclosing the sphere, same radius, and a thin slice through the sphere cutting the cylinder perpendicularly to its axis. By geometry, he showed that the area of cylinder within the slice was (in the limit) the same as the area of sphere surface within the slice.Quarlep said:
Thus, if we consider a band around the sphere between an angle ##\theta## and ##\theta+d\theta## to the cylinder's axis, its surface area is ##2 \pi r \sin(\theta)d\theta##.
But because that band is not all moving in the same direction in your problem, we need to do an integral just to get the KE of that band. Have a go at that.
- #35
Quarlep
- 257
- 4
I didnt understand.
- #36
- 42,802
- 10,495
Take an element on the shell in spherical polar co-ordinates. Write out its KE. If theta is the angle to the line of movement of the shell's mass centre, integrate in a band of width ##rd\theta## for ##\phi## from 0 to ##2\pi##.Quarlep said:
- #37
Quarlep
- 257
- 4
Its too complicated isn't it ?
- #38
- #39
- 42,802
- 10,495
You can make it simpler by recognising that the KE only depends on theta, not phi.Quarlep said:
- #40
Quarlep
- 257
- 4
haruspex said:
Ok, I ll make it simpler but my equation is full correct isn't it ? No mistake Even multiply integral with 2 ...
- #41
- 42,802
- 10,495
Not really. Not sure what your ##v_{\theta}## and ##v_{\phi}## terms are. If they're vectors, they should all be inside the first squared term with v' and vr. I.e. the overall velocity is the sum of four vectors, v' and three velocities relative to v'. But then ##v_{\theta}## and ##v_{\phi}## would both be zero. If they're not vectors, maybe you intend them as the scalar magnitudes of those vectors, in which case the same comment applies.Quarlep said:
So in your equation, throw those two away and expand the remaining squared term. Two of the resulting terms will be independent of theta and phi. The third one, the dot product of v' and vr, will be a function of theta. The integral is then easy.
- #42
mfb
Mentor
- 37,402
- 14,234
Spherical coordinates make this way more complicated.
There is a nice theorem about the kinetic energy of a system if you know the kinetic energy in its center of mass system and the velocity of this center of mass. Both are easy to find here.
If you don't want to use this theorem, you can split the sphere into two parts and derive a special case of the theorem for this sphere.
There is a nice theorem about the kinetic energy of a system if you know the kinetic energy in its center of mass system and the velocity of this center of mass. Both are easy to find here.
If you don't want to use this theorem, you can split the sphere into two parts and derive a special case of the theorem for this sphere.
- #43
Quarlep
- 257
- 4
How I need help.My math is not good enough
- #44
- 42,802
- 10,495
Sure, but the challenge is to resolve the apparent contradiction that Quarlep came up with by using integration methods.mfb said:
I gave Quarlep an easy way using symmetry, but he/she seems to want to do it using a more general approach. Certainly it looks like there is merit in Quarlep having a work-out in integration.
- #45
Quarlep
- 257
- 4
I tried to to use symmetry but again I don't know how to do it.I am worling on
- #46
- 42,802
- 10,495
As I said, just add the KEs of two diametrically opposite points in the shell.Quarlep said:
- #47
Quarlep
- 257
- 4
Yeah you know that I used it find KE of ring shell
- #48
- 42,802
- 10,495
Do you mean in post #31? I didn't realize that's what you had attempted to do there. If it is, you didn't do it right. The two cos terms should have opposite signs and cancel.Quarlep said:
- #49
Quarlep
- 257
- 4
there's one cos isn't it.Or I couldn't see
- #50
- 42,802
- 10,495
The sign of the cos term for one point will be opposite to that on the diametrically opposite point.Quarlep said:
You should have ##(v'+v_r\cos(\theta))^2+(v'-v_r\cos(\theta))^2##, plus the y direction terms.
- #51
- #52
- 42,802
- 10,495
Almost. The m/2 should be a factor of the whole, and the factor 2 you have in front only applies to the sin term.Quarlep said:
- #53
- #54
Quarlep
- 257
- 4
You told me smthing in post 41 but I don't understand it.Thats my fault.I am in high school and my physics is not enough.Thank you very much for support.
- #55
- #56
- 42,802
- 10,495
Yes, that's good, but you don't need to do an integral at all this way. When you expand the terms, all references to theta should disappear, so all the terms are constants.Quarlep said:
- #57
Quarlep
- 257
- 4
Ok,I did it and I found what I found before.
In post 31 I guess m(v^2+v'^2)
In post 31 I guess m(v^2+v'^2)
- #58
- 42,802
- 10,495
You mean, you got the same result as integrating around a circle? Good.Quarlep said:
- #59
Quarlep
- 257
- 4
Yeah
- #60
Quarlep
- 257
- 4
Why don't you guys just not writing the equation