Engineering Find di(0+)/dt and dv(0+)/dt of circuit containing resistor, inductor

[Xhendos]

Homework Statement

Find di(0+)/dt and dv(0+)/dt of circuit containing resistor, inductor and capacitor

Relevant Equations

I = C dv/dt
V = L di/dt

Dear PF,

I am trying to solve practice problem 8.1 and I am stuck on part b which asks us to find di(0+)/dt and dv(0+)/dt.

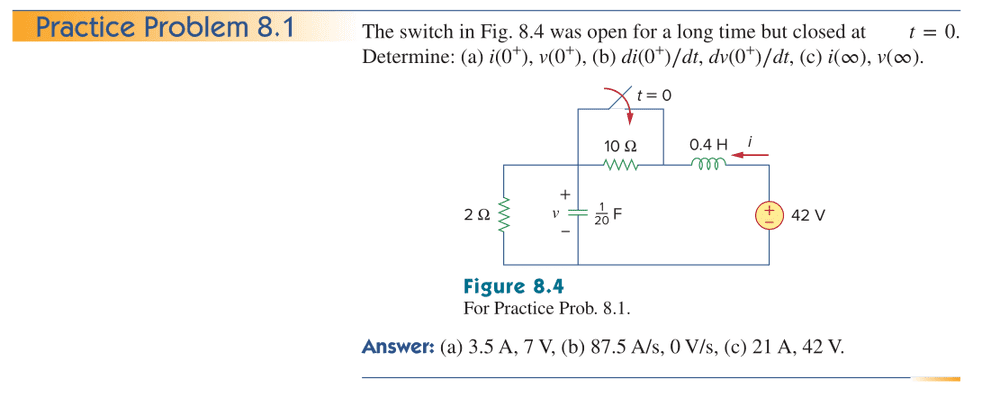
Down below in the picture is my attempt. Before t=0 it is quite intuitive since the inductor acts as short circuit to steady-state DC and a capacitor acts as open circuit to steady-state DC. However, after the switch is closed the circuit got the inductor and a capacitor in series with a 2 ohm resistor. It is very likely that the formules I = C dv/dt and V = L di/dt have to be used but I don't quite know how since the 3.5A current from the inductor wil be spread, a part will go through the 2 ohm resistor and a part will go through the capacitor and I am not quite sure how to analyse this.

Could anyone point me in the right direction to find dv(0+)/dt and di(0+)/dt when the switch just opens?

[Mentor Note -- Adding improved contrast version of the diagram]

 

[BvU]

You have a second order system on your hands. What do you get for $d^2i\over dt^2$ ?
Note: pay attention to the signs !

 

[Xhendos]

You have a second order system on your hands. What do you get for $d^2i\over dt^2$ ?
Note: pay attention to the signs !

To be honest, I do not know. Second order circuits will be covered in the next few chapters. Practice problem 8.1 is asked right after Example 8.1, and in Example 8.1 there is also a second-order circuit but the question only asked for the first derivative right after at t=0+.
The style of this book is that the practice problem is being solved similar to the example problem, so I guess we do not need to know the second derivative of i as of now since there must be a way to solve this question without calculating the second derivative.

 

[BvU]

we do not need to know the second derivative of i as of now since there must be a way to solve this question without calculating the second derivative

Fair enough. Although it's not very complicated: $$ V = L {di\over dt} \ \ i = C {dV\over dt} \ \ \Rightarrow i = LC\, {d^2i \over dt^2} $$-- but I grant you that it may not be very useful here.

More useful $-$ and in the spirit of the exercise and example $-$ is that for $t=0$ the inductor suddenly sees a voltage difference of 35 V, which should be equal to $L {di\over dt}$ so the given answer follows immediately.

Similarly, the inductor counteracts any change in the voltage drop over it (fo a very short tine), so answer d) is 0.