member 731016
- Homework Statement
- The problem I am trying to solve is,
Find the isobaric expansion coefficient ##\frac{dV}{dT}## and the isothermal pressure-volume coefficient ##\frac{dV}{dP}## of a solid that has equation of state ##V+bpT–cT^2=0##
- Relevant Equations
- Equation of state of solid: ##V+bpT–cT^2=0##
The answer to this problem is
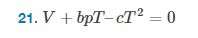
However, I am confused how this relates to the question.
My working is,
##V = cT^2 - bpT##
##\frac{dV}{dT} = 2cT - bp## (I take the partial derivative of volume with respect to temperature to get the isobaric expansion coefficient)
##\frac{dV}{dP} = 0## (I take the partial derivative of volume with respect to pressure to get the isothermal pressure-volume coefficient)
If someone please knows whether I am correct or not then that would be greatly appreciated!
Many thanks!
However, I am confused how this relates to the question.
My working is,
##V = cT^2 - bpT##
##\frac{dV}{dT} = 2cT - bp## (I take the partial derivative of volume with respect to temperature to get the isobaric expansion coefficient)
##\frac{dV}{dP} = 0## (I take the partial derivative of volume with respect to pressure to get the isothermal pressure-volume coefficient)
If someone please knows whether I am correct or not then that would be greatly appreciated!
Many thanks!