Find the charge on the plates a long time after the switch is closed

[Jimmy25]

Homework Statement

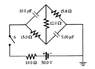
I'm having a problem with the circuit in the attached diagram. I am looking for the charge on the plates of the capacitor a long time after the switch is closed.

Homework Equations

The Attempt at a Solution

I found the current leaving the battery is 0.962 A a long time after the switch is closed. The solution says to multiply this by 27 ohms to find the voltage across the capacitor from which the charge can be calculated. I don't understand how this is possible since the diamond shaped segment is a complex circuit.

 

[emanuel_hr]

A long time after the switch is closed, we have a steady state regime, that is the capacitors are charged up so no current flows through them. You can simply eliminate them from the circuit(mentally) and then calculate the current and the voltage drops between their plates.

Hope this helps.