Krushnaraj Pandya
Gold Member
- 697
- 73
Homework Statement
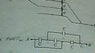
Find equivalent capacitance between A and B of the given figure (pardon camera quality)
Homework Equations
All related
The Attempt at a Solution
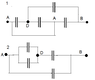
marking junctions, From left to right, starting from original point A-and ending at B I wrote potential at them as follows. A-(A)-(x)-(A)-(B)-B. I labelled the capacitor out of line as C4, and moving from left to right, the ones in line as C1, C2 and C3.
I noticed C1 and C2 are connected across same potential difference and therefore are in parallel connection, I don't know where to place their equivalent capacitor though, I'd appreciate some help, thank you