msrultons
- 3
- 1
- Homework Statement
- find the largest interval on which f is increasing
- Relevant Equations
- Fundamental Theorem of Calculus
Attached here is the full problem I am doing.
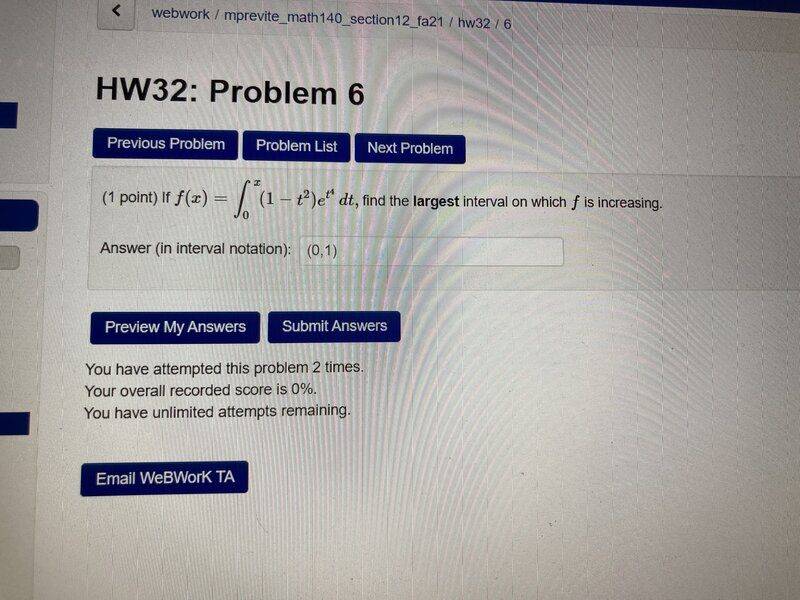
I went through the problem and got my final answer which I thought was correct. Here is my work. They tell me I am wrong. Not sure where is the mistake.
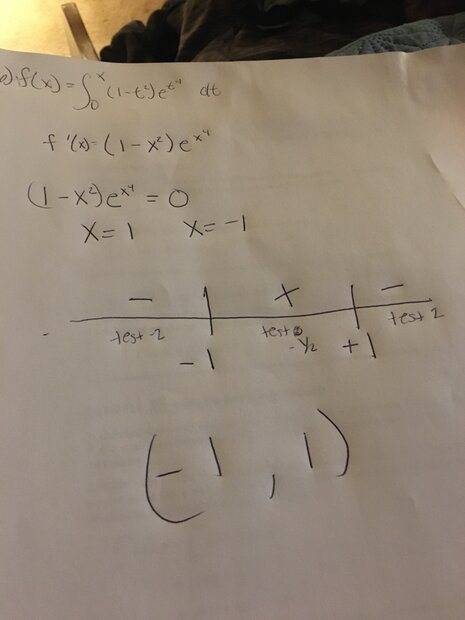
I went through the problem and got my final answer which I thought was correct. Here is my work. They tell me I am wrong. Not sure where is the mistake.