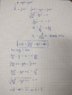- #1
spsch
- 111
- 21
- Homework Statement
- A mass (m=0.2 kg) is suspended from a spring (D/k=10 N/m)
When x = 0 (Spring is relaxed, at equilibrium), v(0) is 3 m/s.
Find v(x) as a first order differential equation.
- Relevant Equations
- I tried using energy conservation to check my work, but I think I messed up. I boxed in my solution. Above is me trying to verify with the conservation of energy and below is my attempt.
Hi all, I have a problem that I've been grappling with for the past 2 hours.
I was confident at first that I found the correct solution, but when I tried to verify I didn't have a constant in my v(x) function.
Here is my attempt:
I appreciate your help kind internet strangers!
I was confident at first that I found the correct solution, but when I tried to verify I didn't have a constant in my v(x) function.
Here is my attempt:
I appreciate your help kind internet strangers!