- #1
cellfoneguy
- 17
- 0
Homework Statement
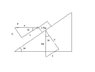
A block is pushed up a frictionless incline by
an applied horizontal force as shown.
The acceleration of gravity is 9.8 m/s2 .
What is the magnitude of the resulting acceleration of the block?
Answer in units of m/s^2.
Homework Equations
Sin(theta)=opposite/hypotenuse
Cos(theta)=adjacent/hypotenuse
Tan(theta)=opposite/adjacent
^^^^^^^^^above equations for a right triangle on a Free Body Diagram
F=ma
The Attempt at a Solution
So if i extend the block's line and make a right triangle with that line and the line of the applied force, i know the theta of that triangle is equal to the ramp's, 34. I can also make a right triangle using gravity and its two vectors, one along the ramp and one perpendicular to the ramp. That triangle's theta is also 34. So to find the acceleration of the block, i need to subtract x from v (See attached picture). But i can't prove the two triangles are congruent, because the gravity vector triangle has only two known values while the force vector triangle has only 1. Help!
Attachments
Last edited: