yoni162
- 16
- 0
Homework Statement
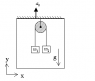
An elevator is accelerating upwards with acceleration a0. Two masses are hanging down from a pulley, connected to each other. I need to find the acceleration of m1, as viewed from within the elevator.
Homework Equations
The Attempt at a Solution
If I look at each mass separately, each one is subjected to 3 forces: mg, T, and ma0, when T is obviously pointed upwards, and mg & ma0 are pointed downwards..
Now, if I want to find a1 --> m1's acceleration as viewed from within the elevator, I write:
m1
T-m1g-m1a0=m1a1
When I'm assuming a1 is in the positive direction of the Y axis. Now to m2:
m2
m2g+m2a0-T=m2a2
When I'm assuming that a2 will be in the opposite direction of the Y axis (since m1 will go up, m2 will go down). That's why I write forces the are in the positive direction of Y with a (-) before them, and forces which are directed in the negative direction of Y with a + before them. I know that's only a guess, but if I'm wrong and m1 will go down, a1 will turn out to be negative, no? I've used this method when solving 'inertial' problems and it works..
Also, I'm assuming the a1=-a2, again, like in 'inertial' situations..only here I'm not so sure..is this assumption true? Because when I solve the equations like they are now, I get that:
(m2-m1)(a0+g)=a1(m1-m2)
a1=-a0-g
Which isn't true according tow the answers..where am I wrong?