PhysHobbiest
- 7
- 3
- Homework Statement
- As the title says, I was simply looking to geometrically find the angular speed of an object traveling along a line on the x axis with respect to a position at a height h on the z axis.
- Relevant Equations
- tan(θ) = x/h
So clearly the easiest way to relate the angular speed to the linear speed would be to start from ##\tan(θ) = x/h## and take a time derivative of both sides. However, it also shouldn't be difficult to find the angular speed geometrically. Using the diagram below one can see that:
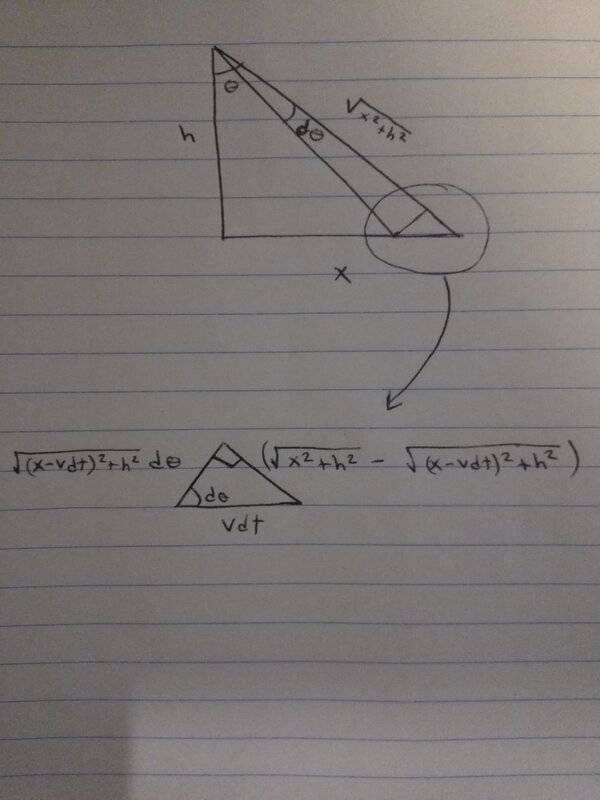
##sin(dθ) = \frac {{\sqrt {x^2+h^2}}-{\sqrt {(x-vdt)^2+h^2}}} {vdt}##
which is approximately (after a small angle approx and using the definition of the derivative)
##dθ = \frac {d} {dx} \sqrt {x^2+h^2}##
which yields
##dθ = \frac {x} {\sqrt {x^2+h^2}}##
Now this I believe is nonsense, and I'm having difficulty figuring out exactly what went wrong. Did I mess up along the way, or were the approximations I made not good ones? My guess is any approximation that would leave an infinitesimal value on only one side of the equation is a bad one. Just looking for confirmation here.
##sin(dθ) = \frac {{\sqrt {x^2+h^2}}-{\sqrt {(x-vdt)^2+h^2}}} {vdt}##
which is approximately (after a small angle approx and using the definition of the derivative)
##dθ = \frac {d} {dx} \sqrt {x^2+h^2}##
which yields
##dθ = \frac {x} {\sqrt {x^2+h^2}}##
Now this I believe is nonsense, and I'm having difficulty figuring out exactly what went wrong. Did I mess up along the way, or were the approximations I made not good ones? My guess is any approximation that would leave an infinitesimal value on only one side of the equation is a bad one. Just looking for confirmation here.
Last edited: