Finding magnitude and direction of net torque on a dipole

AI Thread Summary
To find the net torque on a dipole with charges of ±3.0 microcoulombs separated by 3.20 nm in an electric field of 8000 N/C, the force is calculated as F = 2.4E-2 N. The effective lever arm is determined using l = 1.84E-9 m. The net torque is then computed using the formula T = qEl, leading to the conclusion that the torque acts in a specific direction, either clockwise or counterclockwise. The calculations confirm the relationship between force, lever arm, and torque in this context. The final answer provides the magnitude and direction of the net torque on the dipole.
ick84
Messages
2
Reaction score
0

Homework Statement



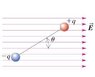
For the dipole shown, the charges are ± 3.0 micro coulombs separated by a distance of 3.20 nm and oriented so that the theta is 35.0 degrees. If the electric field has a magnitude of 8000 N/C, find the magnitude and direction (clockwise/counterclockwise) of the net torque on the dipole about the same axis as before.


Homework Equations



F = qE
torque = Fl

The Attempt at a Solution



first i solved for F = (3.0E-6 C)(8000N/C) = 2.4E-2 N

then solved for l = (3.20nm)(sin35) = 1.84E-9

net torque = 2 * F * l ??
 

Attachments

  • 1027679.jpg
    1027679.jpg
    7.1 KB · Views: 676
Physics news on Phys.org
NVM i solved it...

T = Fl
T = qEl
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Three equal forces applied to a rectangle, find net torque direction?
Replies
30
Views
3K
Calculate the magnitude and direction of the torque
Replies
1
Views
2K
Are the 2nd and 3rd problems in this video correctly solved? (charged dipole and organ pipe problems)
Replies
3
Views
969
Effect of different magnetic fields on a magnetic dipole
Replies
25
Views
1K
Finding magnitude and direction of net force on a dipole.
Replies
4
Views
7K
Where on a rigid body is a resultant force applied?
Replies
11
Views
1K
What is the torque on an electric dipole in an electric field?
Replies
2
Views
2K
Finding the net torque about the axle?
Replies
3
Views
5K
Direction of friction in yo-yo where applied force is at top
Replies
8
Views
2K
Calculating Net Torque on Wheel Axle
Replies
7
Views
4K

Hot Threads

Recent Insights

Back
Top