ryao3688
- 4
- 1
(Moved to the homework section by moderator.)
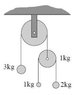
Please see the image. My confusion is with a moveable pulley. Can I just do my balances on both 1kg and 2kg masses disregarding the acceleration of the pulley? Here are my eqns. Object numbers 1, 2 and 3 denote the 3kg, 1kg and 2 kg weights. 4 is the moveable pulley. T1 is the string on the upper left, T2 for the lower right string tension. Let's say up is neg, down is positive.
ma = sum of F's for all
m1a1 = m1g - T1
m2a2 = m2g - T2
m3a3 = m3g - T2
m4a4 = 2T2 - T1 + m4g
But I know that a1= -a4 and a2= -a3 since if the pulley moves one way with an object, the other one must travel in opposite direction with same acceleration.
You sub that in, you get four eqns and four unknowns and I can easily solve. But my confusion is really with that moveable pulley. I included its weight in the eqn. Do I need to include its acceleration into objects 2 and 3? Did I make any mistake? Thanks.
Please see the image. My confusion is with a moveable pulley. Can I just do my balances on both 1kg and 2kg masses disregarding the acceleration of the pulley? Here are my eqns. Object numbers 1, 2 and 3 denote the 3kg, 1kg and 2 kg weights. 4 is the moveable pulley. T1 is the string on the upper left, T2 for the lower right string tension. Let's say up is neg, down is positive.
ma = sum of F's for all
m1a1 = m1g - T1
m2a2 = m2g - T2
m3a3 = m3g - T2
m4a4 = 2T2 - T1 + m4g
But I know that a1= -a4 and a2= -a3 since if the pulley moves one way with an object, the other one must travel in opposite direction with same acceleration.
You sub that in, you get four eqns and four unknowns and I can easily solve. But my confusion is really with that moveable pulley. I included its weight in the eqn. Do I need to include its acceleration into objects 2 and 3? Did I make any mistake? Thanks.
Attachments
Last edited by a moderator: