Finding the filtered output signal

[hxluo]

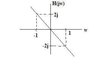
A causal LTI filter has the frequency response H(jw) shown in the graph. For each of these input signals, determine the filtered output signal y(t).

1) x(t)=exp(jt)

2) x(t)=(sin(wt))u(t)

3) X(jw)= 1 / ((jw)(6+jw))

4) X(jw)= 1 / (2+jw)

I don't understand what I have to do to find y(t), any help is appreciated, thanks

 

[rbj]

what is the function description of $H(j \omega)$? can you extract that out of the graph?

 

[hxluo]

nothing much in the graph, just a straight line from (-1, 2j) to (1, -2j)

 

[LeBrad]

There are many ways to find y(t):
y(t) = h(t) * x(t) convolution
y(t) = F(H(jw)X(jw)) Fourier transform of Y(jw)
y(t) = H(jw)x(t) amplitude scaling if x is an eigenfunction

Which one is most applicable? Or which have you learned?

 

[hxluo]

yes, i learned it before, so is it correct to say H(jw)= -w?

 

[Einstienear]

y"t" = h(t) * x(t)
y"t" = f(H(jw)X(jw)
y"t" = h(jw)x(t)