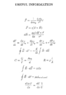Tomi Kolawole
- 30
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
I soled for the integral of the magnetic field but i don't know what bounds to intergrate over and also i what is DS in this case? its a point charge so shouldn't bio savart have q(v*b) instead of i(ds*r)?[/B]