Engineering Finding the Thevenin equivalent circuit.

AI Thread Summary
The discussion focuses on finding the Thevenin equivalent circuit to maximize power transfer to a resistor. The original poster attempted to calculate the Thevenin resistance (Rth) using nodal analysis but arrived at an incorrect negative value, indicating a mistake in their approach. Participants pointed out that the circuit was analyzed incorrectly, specifically that the load resistor was not properly accounted for when determining the open circuit voltage and short-circuit current. They emphasized the importance of keeping dependent sources intact during analysis and suggested using mesh analysis for a clearer solution. Ultimately, it was noted that a correct calculation of Rth should yield a positive value, with one participant mentioning a specific value of 104.75 ohms when done correctly.
Mr.Sure
Messages
8
Reaction score
0

Homework Statement


Find resistance R so that maximum power is transferred to this resistor.

http://i.imgur.com/XsxTFCq.png
upload_2018-11-24_21-49-32.png


Homework Equations



Rth = Voc/Isc

The Attempt at a Solution



I tried to find the Thevenin equivalent circuit across the resistor R because the Thevenin resistance must be equal to the load resistor in order for maximum power to be transferred.

I replaced R with an open circuit to find the open circuit voltage.
Using Nodal Analysis, I obtained the equation: (V1 - 4V)/5 + V1/15 = 0
So, V1 = 3 = Voc.

Then I redrew the circuit and replaced R with a short circuit and solved for two voltages at the nodes.

http://i.imgur.com/247x27x.pngI used Nodal Analysis and obtained two equations.

[3Vx = V2/6]

(V1-4V)/5 + V1/15 + V2/2 + (V1-V2)/5 = 0

V2/6 + (V2-V1)/5 = 3V2/6

I got V1 = 48V, V2 = -72V and Isc = V2/6 = -12A

so I got Rth = 3/-12 = -0.25 ohms.

This isn't right, but I"m not sure what I did wrong.
 
Physics news on Phys.org
That's an unnecessarily awkward way to the Rth. Just do what you are supposed to do to the current and voltage sources (you do know what that is, I assume) and you get a very simple resistive circuit that simplifies quite easily to Rth. Your Rth is WAY off, as should be obvious from (1) the fact that it's negative and (2) the fact that it is so small.

EDIT ... I missed that you had redrawn the circuit. you did it completely incorrectly. You threw away the load resistor and are now finding the equivalent circuit for something that is not what was asked for.

EDIT, EDIT ... I see that the question at the top of the post is NOT the question in the title. I was using the question in the title and shooting for the Thevenin equivalent circuit.
 
Sorry about that. I was originally going to ask for help on another problem, but I solved it. I forgot to change the title. Also, I'm pretty sure I got the right answer for the Thevenin voltage.
 
Mr.Sure said:
Sorry about that. I was originally going to ask for help on another problem, but I solved it. I forgot to change the title. Also, I'm pretty sure I got the right answer for the Thevenin voltage.

Since I don't see any statement of what you got for Rth, I can't comment on that.

You have not addressed my statement that you seem to be getting the Thevenin equivalent for the wrong circuit.
 
phinds said:
That's an unnecessarily awkward way to the Rth. Just do what you are supposed to do to the current and voltage sources (you do know what that is, I assume) and you get a very simple resistive circuit that simplifies quite easily to Rth

Do you mean turn off the independent sources and simply combine the resistors? I'm pretty sure you can't do that when there is a dependent source.


phinds said:
Since I don't see any statement of what you got for Rth, I can't comment on that.

You have not addressed my statement that you seem to be getting the Thevenin equivalent for the wrong circuit.

Why is it for the wrong circuit?
 
OK, I missed the fact that the current source is dependant.

It's for the wrong circuit because it's not across the load resistor.
 
How is it not for the load resistor? Doesn't the TEC process involve removing the component and measuring the voltage across an open terminal and current through a short circuit?
 
Removing the load resistor does not mean shorting it out, it means leaving it open. Also, in your redrawn circuit, I'm assuming you are finding the equivalent circuit between the nodes you have labeled V1 and V2. This is not across the load resistor.
 
I forgot to post the redrawn circuit when I was finding the open circuit voltage.

So V1 just ends up being V thevenin.

http://i.imgur.com/fiTZJnl.png

In this circuit: http://i.imgur.com/247x27x.png
I labeled 2 nodes because I was trying to determine the current flowing through the wire I replaced the load resistor with.
 
  • #10
You might find it easier to use mesh analysis on this circuit. One of the meshes has a constrained current which is wholly dependent upon the current in the "output" loop. So you have two loop currents to solve for, and you only need one of them.

attachment.php?attachmentid=62534&stc=1&d=1381061289.gif


The voltage across the load resistor is ##i_2 R##. Rearrange the resulting expression to the form of a voltage divider and pick out the Thevenin model components.
 

Attachments

  • Fig1.gif
    Fig1.gif
    4.8 KB · Views: 726
  • #11
I've already found the Thevenin Voltage what other value would I get by solving it that way?
 
  • #12
Mr.Sure said:
I've already found the Thevenin Voltage what other value would I get by solving it that way?

1) The circuit remains intact so you don't have to worry that removing the load alters some "dependent" characteristic of the circuit. For example, in this circuit opening the load "kills" the sensor that defines Vx and disables the dependent current source. So no fiddling about with applying external sources to stimulate the circuit.

2) You need to solve only once to obtain both Vth and Rth at the same time.

How's that? :smile:
 
  • #13
Wouldn't this problem have 3 unknowns and 2 equations? Also, my teacher just sent the answer. I don't understand how he did it. The steps he used to solve the circuit contradict what's written in my textbook.

http://i.imgur.com/Pb8Zr1C.png
 
  • #14
Mr.Sure said:
Wouldn't this problem have 3 unknowns and 2 equations? Also, my teacher just sent the answer. I don't understand how he did it. The steps he used to solve the circuit contradict what's written in my textbook.

http://i.imgur.com/Pb8Zr1C.png

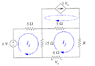
No, the mesh equations have two unknowns: the currents in the two lower loops. The current in the upper loop is entirely determined by the current in the lower right loop, since its "sense" resistor is located there. It's a straightforward substitution as you write the loop equations.

The "by the book" procedure for finding the Thevenin model is to: 1) remove the load and find the open circuit voltage presented at the open terminals, and 2) Either determine the equivalent resistance with the sources suppressed, or short-circuit the output and determine the short-circuit current, with the Thevenin resistance will be given by ##V_{th}/I_{short-circuit}##. All of the above can be foiled by dependent sources that get disrupted by interfering with the load.

In order to find Rth your teacher had to insert the external 1A source in place of the load in order to "stimulate" the circuit's dependent source, a procedure I alluded to before. By leaving the circuit intact and solving the mesh equations you can avoid that...

If you think about the form of a Thevenin equivalent model with a load attached, it forms a classic voltage divider: a voltage source with a series resistance and a load. The equation representing such a situation is
$$ V_{load} = V_{th}\frac{R_L}{R_L + R_{th}}$$
After you solve the mesh equation for the current through the load you multiply by the load resistor R to find the load voltage. The resulting expression can be arranged in the same form as the voltage divider equation above, and the Thevenin voltage and resistance read directly from the equation.

You could also use nodal analysis. Any method that will let you solve for the voltage across the load resistor R will do. I picked mesh analysis largely due to experience... the load current through R is identical to one of the mesh currents, so no fiddling about later to calculate the current from node potentials.
 
  • #15
Mr.Sure said:
Wouldn't this problem have 3 unknowns and 2 equations? Also, my teacher just sent the answer. I don't understand how he did it. The steps he used to solve the circuit contradict what's written in my textbook.

http://i.imgur.com/Pb8Zr1C.png

Your professor didn't indicate on his schematic for the Rth calculation where his reference node (ground) was, but it's apparently the left end of the 6 ohm resistor. The voltages V1 and V2 are calculated with respect to this node. When he calculates V2/I, he is not using the voltage across the 1 amp source he applied in place of the resistor R; rather, he is using the voltage across the series combination of the 1 amp source and the 6 ohm resistor.. Furthermore, he didn't set the 4 volt source to zero for this calculation, either. Thus, he gets the wrong value for Rth.

If the calculation is done without these two errors, a value of 104.75 ohms is obtained for Rth.
 

Similar threads

Thevenin Theorum
Replies
1
Views
1K
Engineering How to Calculate Thevenin Equivalent Circuit
Replies
5
Views
2K
Engineering Find the Thevenin equivalent circuit
Replies
42
Views
6K
Thevenin Equivalent : Wrong value for Rth
Replies
7
Views
3K
Engineering Finding the Thevenin Equivalent Circuit for a Network with a Load Resistor
Replies
1
Views
2K
Engineering Calculating Norton Equivalent Circuit for Complex Load Impedance
Replies
2
Views
2K
Are My Thevenin and Norton Equivalent Calculations Correct?
Replies
5
Views
2K
How Do You Calculate Thevenin Equivalent Circuits?
Replies
5
Views
1K
Engineering Norton/Thevenin Equivalent circuits with a dependent voltage source
Replies
9
Views
5K
Engineering Find the Thevenin Equivalent circuit
Replies
35
Views
6K

Hot Threads

Recent Insights

Back
Top