Poulsen8r
- 2
- 0
Homework Statement
Hi, this question is from Fundamentals of Physics 8th Edition:
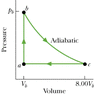
Figure 20-27 shows a reversible cycle through which 1.00 mole of a monatomic ideal gas is taken. Process bc is an adiabatic expansion, with pb = 5.20 atm and Vb = 4.80 x 10-3 m3. For the cycle, find (a) the energy added to the gas as heat, (b) the energy leaving the gas as heat, (c) the net work done by the gas, and (d) the efficiency of the cycle.
(Figure is Attached)
Homework Equations
PiVi^(Gamma)=PfVf^(Gamma)
W=P(delta)V
PV=nRT
PV^(Gamma)=nRTV^(Gamma-1)
(Delta)U=Q-W
Q=nCp(Delta)T
(Gamma)= 1.67 for monoatomic gas
Eint=(3/2)nRT
The Attempt at a Solution
This may look a little weird because of the subscript and powers but i'll give it a go:
Calculating Pressure at (a) and (c):
PiVi^(Gamma)=PfVf^(Gamma)
5.2689e5*4.8e-3=Pf*38.4e-3
Pf=1.6352e4 Pascals
Calculating Work from c to a:
W=P(delta)V
=1.6352e4*(38.4-4.8)e-3
=549.4272J
I believe this is correct...
Calculating temperature at (b) and (c):
T=(PV^(Gamma))/(nRV^(Gamma-1))
Tb=((5.2689e5)*(4.8e-3)^1.67)/(1*8.314*(4.8e-3)^(-0.67))
=304.1944K
Tc=((1.6352e4)*(38.4e-3)^1.67)/(1*8.314*(38.4e-3)^(-0.67))
=75.5233K
Calculating (Delta)Eint for process b to c:
(Delta)Eint=nRTf-nRTi
=nRTc-nRTb
=(1*8.324*75.5233)-(1*8.314*304.1944)
=-2851.757J --> I think this is where the problem lies.
Calculating work for process b to c:
(Delta)Eint=Q-W, as it is adiabatic Q=0 therefore (Delta)Eint=-W.
W=2851.757J
As there is no work for the process a to b, this means that the net work done on the system is 3401.18J... Which is incorrect... I don't know the solution but i know that that answer is wrong... I tried a few other methods than the one above but i get the same answer and i am going crazy and in circles...