- #1
pobatso
- 17
- 0
Hi all, got a Control question here, and I'm struggling with what I assume is a simple algebraic step. Thanks in advance!
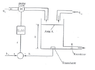
A closed loop control system governs the level of water in a tank (H(s)) to meet a target height (Hi(S)). The flow of water into the tank is controlled by a transducer that feeds the current level of the tank into a differencing junction that works out the error (H(s)-Hi(s)). The flow rate of water pumped in is proportional to this error, with gain K.
The flow out of the tank is also constrained by a linearized flow restrictor, with flow out equal to the height/constant (Qd=H(s)/R).
There is also an additional flow into the tank from a separate pipe, with flow rate Qd.
The question is to find the transfer function, time constant and steady state gain. I've attached a diagram.
So far I've gotten as far as the governing equation:
Qi + Qd - Qo = A.dH(t)/Dt
Laplace: Qi(s) + Qd(s) - Qo(s) = A.s.H(s)
Where Qi = Flow in
Qd = Additional disturbance flow
Qo = Flow out
A = XSection area of tank
Using the information about the individual components this goes to:
K.Hi(s) - K.H(s) + Qd(s) - H(s)/R = A.s.H(s)
The correct way to describe transfer function (Checked with answer booklet):
H(s)=(R.K.Hi + R.Qd(s)) / (R.k +R.A.s + 1)
But I can't get the hang of expressing it in a way that would allow me to get the specific time function, ie I can't arrange it into form H(s)/Hi(s)=u/(1+Ts) where u is the SS Gain and T is the time constant.
Any help with this step would be fab!
Regards
Homework Statement
A closed loop control system governs the level of water in a tank (H(s)) to meet a target height (Hi(S)). The flow of water into the tank is controlled by a transducer that feeds the current level of the tank into a differencing junction that works out the error (H(s)-Hi(s)). The flow rate of water pumped in is proportional to this error, with gain K.
The flow out of the tank is also constrained by a linearized flow restrictor, with flow out equal to the height/constant (Qd=H(s)/R).
There is also an additional flow into the tank from a separate pipe, with flow rate Qd.
The question is to find the transfer function, time constant and steady state gain. I've attached a diagram.
Homework Equations
The Attempt at a Solution
So far I've gotten as far as the governing equation:
Qi + Qd - Qo = A.dH(t)/Dt
Laplace: Qi(s) + Qd(s) - Qo(s) = A.s.H(s)
Where Qi = Flow in
Qd = Additional disturbance flow
Qo = Flow out
A = XSection area of tank
Using the information about the individual components this goes to:
K.Hi(s) - K.H(s) + Qd(s) - H(s)/R = A.s.H(s)
The correct way to describe transfer function (Checked with answer booklet):
H(s)=(R.K.Hi + R.Qd(s)) / (R.k +R.A.s + 1)
But I can't get the hang of expressing it in a way that would allow me to get the specific time function, ie I can't arrange it into form H(s)/Hi(s)=u/(1+Ts) where u is the SS Gain and T is the time constant.
Any help with this step would be fab!
Regards