Gyro
- 49
- 0
Hello everyone,
Thank you to all who offer their help.
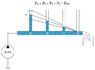
If the volumetric output of the pump were increased, keeping the pipe diameter constant, would the pressures at A, B, and C increase or decrease? Would the heights within each column at each location rise or fall? Explain.
If smaller pipe were used, keeping pump volumetric output the same, would the pressures at A, B, and C increase or decrease? How would the heights of each column change? Explain.
Flow rate = Area x Velocity [1]
Bernoulli's energy balance: KE1 + PE1 + GPE1 = KE2 + PE2 + GPE2 [2]
where
KE = kinetic energy, PE = potential energy (from pressurized fluid), GPE = gravitational potential energy (from height difference from reference point)
My answer follows:
In the first situation, when pump volumetric output is increased:
From [1]: if Flow rate increases, and Area is const., then Velocity increases.
From [2]: if Velocity increases, KE increases, so KE2 - KE1 = some value
since there is no height change along the pipe, GPE2 - GPE1 = 0
so to balance energies, a decrease in PE must occur, which means a decrease in the pressure.
Therefore, an increase in pump volumetric flow will decrease the pressures at A, B, and C and thus make the heights of each column fall accordingly.
In the second situation, when volumetric output is const., and diameter of pipe is reduced:
From [1]: if Area is decreased, and Flow rate const., then Velocity increases, as in the first situation. Again, KE increases, GPE const., PE has to decrease, and pressures decrease. Again, the heights of liquid fall for each column. Situation 1 and 2 both increase fluid velocity, which drops pressure, according to Bernoulli, and the heights will fall.Problem is, the answer says the pressures and heights increase at all locations (except D as it is at atmospheric pressure) for both scenarios.
What am I not understanding? Any help is appreciated.
Thank you to all who offer their help.
Homework Statement
If the volumetric output of the pump were increased, keeping the pipe diameter constant, would the pressures at A, B, and C increase or decrease? Would the heights within each column at each location rise or fall? Explain.
If smaller pipe were used, keeping pump volumetric output the same, would the pressures at A, B, and C increase or decrease? How would the heights of each column change? Explain.
Homework Equations
Flow rate = Area x Velocity [1]
Bernoulli's energy balance: KE1 + PE1 + GPE1 = KE2 + PE2 + GPE2 [2]
where
KE = kinetic energy, PE = potential energy (from pressurized fluid), GPE = gravitational potential energy (from height difference from reference point)
The Attempt at a Solution
My answer follows:
In the first situation, when pump volumetric output is increased:
From [1]: if Flow rate increases, and Area is const., then Velocity increases.
From [2]: if Velocity increases, KE increases, so KE2 - KE1 = some value
since there is no height change along the pipe, GPE2 - GPE1 = 0
so to balance energies, a decrease in PE must occur, which means a decrease in the pressure.
Therefore, an increase in pump volumetric flow will decrease the pressures at A, B, and C and thus make the heights of each column fall accordingly.
In the second situation, when volumetric output is const., and diameter of pipe is reduced:
From [1]: if Area is decreased, and Flow rate const., then Velocity increases, as in the first situation. Again, KE increases, GPE const., PE has to decrease, and pressures decrease. Again, the heights of liquid fall for each column. Situation 1 and 2 both increase fluid velocity, which drops pressure, according to Bernoulli, and the heights will fall.Problem is, the answer says the pressures and heights increase at all locations (except D as it is at atmospheric pressure) for both scenarios.
What am I not understanding? Any help is appreciated.
Attachments
Last edited: