cwill53
- 220
- 40
- Homework Statement
- 1.3 Force from a cone ** (a) A charge q is located at the tip of a hollow cone (such as an ice
cream cone without the ice cream) with surface charge density
σ. The slant height of the cone is L, and the half-angle at the
vertex is θ. What can you say about the force on the charge q
due to the cone?
(b) If the top half of the cone is removed and thrown away , what is the force on the charge q due to the remaining part of the cone? For what angle θ is this force maximum?
- Relevant Equations
- $$\vec{F}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\hat{r}_{0j}}{r^{2}_{0j}}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\vec{r}_{0j}}{r^{2}_{0j}}\frac{1}{\left \|\vec{r}_{0j} \right \|}$$
This is the diagram I drew for my calculations:
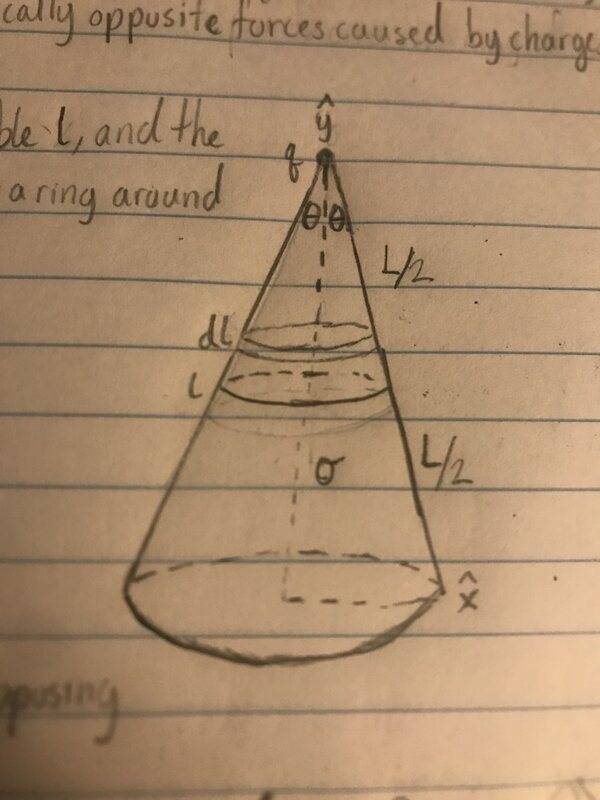
I wanted to see if my work for part (a) makes sense.
If there is a variable ##l## that runs along the slant of total length ##L##, a ring around the cone can have an infinitesimal thickness ##dl##.
By Coulomb's law,
$$\vec{F}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\hat{r}_{0j}}{r^{2}_{0j}}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\vec{r}_{0j}}{r^{2}_{0j}}\frac{1}{\left \|\vec{r}_{0j} \right \|}$$
The symmetry of the cone can be used to show that the horizontal components of forces along the ##\hat{x}## direction cancel by considering two charges on the ring ##dQ## on opposite sides of one another. The sum of the forces of these charges on the charge q at the tip of the cone is
$$\vec{F}=\frac{1}{4\pi \varepsilon _0}(\frac{dQq\left \langle lsin\theta ,lcos\theta \right \rangle}{((lsin\theta )^2+(lcos\theta )^2)^{\frac{3}{2}}}+\frac{dQq\left \langle -lsin\theta ,lcos\theta \right \rangle}{((lsin\theta )^2+(lcos\theta )^2)^{\frac{3}{2}}}$$
$$\Rightarrow \vec{F}=\frac{2dQqlcos\theta }{4\pi \varepsilon _0l^{3}}\hat{j}$$
For the total force on q caused by the ring, I wrote
$$\vec{F}_{ring}=\frac{1}{4\pi \varepsilon _0}\sum_{i=1}^{N}\frac{dQ_iqlcos\theta }{4\pi \varepsilon _0l^3}\hat{j}$$
where N is the number of charges dQ on the ring.
Since there is a surface charge density σ, I wrote that the surface area can be written as
$$2\pi (lsin\theta )dl\Rightarrow q_{ring}=\sigma 2\pi (lsin\theta )dl$$
The total force is the sum of the forces of all the rings of infinitesimal thickness ##dl## that make up the cone:
$$F_{cone}=\int_{0}^{L}\frac{q\sigma 2\pi (lsin\theta )lcos\theta }{4\pi \varepsilon _0l^3}\hat{j}dl$$
I assume part (b) could be done by just integrating from 0 to L/2, but I wanted to make sure this part made sense.
I wanted to see if my work for part (a) makes sense.
If there is a variable ##l## that runs along the slant of total length ##L##, a ring around the cone can have an infinitesimal thickness ##dl##.
By Coulomb's law,
$$\vec{F}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\hat{r}_{0j}}{r^{2}_{0j}}=\frac{1}{4\pi \varepsilon _0}\sum_{j=1}^{N}\frac{q_0q_j\vec{r}_{0j}}{r^{2}_{0j}}\frac{1}{\left \|\vec{r}_{0j} \right \|}$$
The symmetry of the cone can be used to show that the horizontal components of forces along the ##\hat{x}## direction cancel by considering two charges on the ring ##dQ## on opposite sides of one another. The sum of the forces of these charges on the charge q at the tip of the cone is
$$\vec{F}=\frac{1}{4\pi \varepsilon _0}(\frac{dQq\left \langle lsin\theta ,lcos\theta \right \rangle}{((lsin\theta )^2+(lcos\theta )^2)^{\frac{3}{2}}}+\frac{dQq\left \langle -lsin\theta ,lcos\theta \right \rangle}{((lsin\theta )^2+(lcos\theta )^2)^{\frac{3}{2}}}$$
$$\Rightarrow \vec{F}=\frac{2dQqlcos\theta }{4\pi \varepsilon _0l^{3}}\hat{j}$$
For the total force on q caused by the ring, I wrote
$$\vec{F}_{ring}=\frac{1}{4\pi \varepsilon _0}\sum_{i=1}^{N}\frac{dQ_iqlcos\theta }{4\pi \varepsilon _0l^3}\hat{j}$$
where N is the number of charges dQ on the ring.
Since there is a surface charge density σ, I wrote that the surface area can be written as
$$2\pi (lsin\theta )dl\Rightarrow q_{ring}=\sigma 2\pi (lsin\theta )dl$$
The total force is the sum of the forces of all the rings of infinitesimal thickness ##dl## that make up the cone:
$$F_{cone}=\int_{0}^{L}\frac{q\sigma 2\pi (lsin\theta )lcos\theta }{4\pi \varepsilon _0l^3}\hat{j}dl$$
I assume part (b) could be done by just integrating from 0 to L/2, but I wanted to make sure this part made sense.