Free body diagram and applying Newtons law

[nilly]

hello! this is a question that iv been working on and can't seem to figure it out, i checked out the other two threads on this same question but they were of no help, anyway here it is:

A wedge with mass M rests on a frictionless horizontal table top. A block with mass m is placed on the wedge There is no friction between the block and the wedge. The system is released from rest.
http://tinyurl.com/9zcf7uq
questions: 1.
Calculate the acceleration of the wedge.
Express your answer in terms of M, m, α, and constant g.

2.
Calculate the horizontal component of the acceleration of the block.
Express your answer in terms of M, m, α, and constant g.

3.
Calculate the vertical component of the acceleration of the block.
Express your answer in terms of M, m, α, and constant g.

attempt at solution:

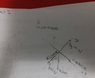
i drew the two free body diagrams and put in the forces.for the mass i have a normal force from wedge up in +y direction and Wcos (theta) down in -y direction, and Wsin(theta) in +x direction

for the wedge i have the normal of ground on wedge in +y direction, normal of block on wedge in -y direction and Wcos(theta) also in - y direction. and for the +x direction i have Wsin (theta)

and i know there is no movement in the y direction so i equated that to zero..

i write the equations for the y and x components down and equate them to get accelaration but i keep getting the wrong answer, help please?

 

[Chestermiller]

Let's see more detail on what you did. The velocity of the block is zero in the y direction (this is incorrect, and has been corrected in post #4), but the velocity of the wedge is not. Also, the normal force of the ground on the wedge is not in the +y direction (assuming y is the direction normal to the incline).

chet

 

[nilly]

why is the velocity of the wedge not zero in the y direction?i think i may have drawn my free body diagrams incorrectly, which may be the reason that i am not able to get the right answers. i have attached a picture of my free body diagrams

 

[Chestermiller]

why is the velocity of the wedge not zero in the y direction?i think i may have drawn my free body diagrams incorrectly, which may be the reason that i am not able to get the right answers. i have attached a picture of my free body diagrams

The velocity of the wedge is zero in the vertical direction, which is not the y direction. I also made a mistake in my previous post when I said that the velocity of the block is zero in the y direction. The component of the block velocity relative to the wedge is zero in the y direction normal to the slope. But the wedge is moving in the horizontal direction, and thus has components in the directions parallel and perpendicular to the slope.

It might be easier to set this problem up by doing the balances in the horizontal and vertical directions, rather than in the directions perpendicular and parallel to the incline. Try doing this and see what you get.

I'll look over what you did later today.

Chet

 

[Chestermiller]

I'm not able to follow your diagrams. Please try to set up the problem with the coordinate axes horizontal and vertical, not perpendicular and parallel to the incline.

Do you understand yet why the wedge velocity is not zero in the direction perpendicular to the incline, and why the normal force by the ground on the wedge is not pointed in the direction perpendicular to the incline?

Chet