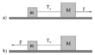
- #1
SakuRERE
- 68
- 5
Homework Statement
In the figure above a block of mass m is connected to a block of mass M > m by a string. Both blocks sit on a smooth surface with a coefficient of kinetic friction µk between either block and the surface. In figure a), a force of magnitude F (large enough to cause both blocks to slide) is exerted on block M to pull the system to the right. In figure b), a force of (the same) magnitude F is exerted on block m to pull the system to the left. Circle the true statement:
a) The tension Ta > Tb.
b) The tension Ta < Tb.
c) The tension Ta = Tb.
d) There is not enough information to determine the relative tension in the two cases.
known data:
we know that both blocks have the same coefficient of friction and that their masses are different.
Homework Equations
ΣF= ma
μk= Fk*N
The Attempt at a Solution
I drew first the FBD of both block in each situation and wrote the equation. for the first situation (a)
Block M has this equation:
ΣF= ma
F-Ta-Fk=Ma
Ta=F-Fk-Ma
Ta=F-μkMg-Ma
while block m I ended up with:
Ta=ma+μkmg
and for the second situation:
block M equation:
Tb= Ma+μkMg
and block m:
Tb=F-μkmg-ma
so I said since larger mass has larger KInetic Friction Fk, compared to the small one, and because of comparing the Ta equation of M and the Tb equation of M then Tb I guess is bigger.
I don't know if I