Friction problem on cube of mass

[braindead101]

a very small cube of mass m is placed on the inside wall of a funnel. The wall of the funnel makes an angle theta with the vertical axis of rotation (dotted line). The center of the cube is a distance r from the axis of rotation. the cube is held by static friciton. The funnel is then rotated about a vertical axis at an angular speed of w (omega). it is found that the angular speed can be increased to a maximum value w(max) (omega max) at which point the cube is no longer held by the static frictional force and it flies out of the funnel. calculate w(max)

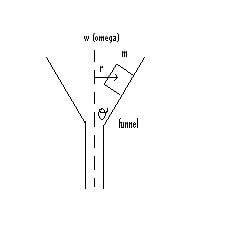
i separated everything into x and y components, but i think i did this wrong
i got equations
Fstatic - Fg cos theta = mw(max)^2r
Fn - Fg sin theta = ma
am i suppose to set a to zero? and are those even right to begin with

 

[andrevdh]

It helps to make a drawing with the forces an angles on it.

 

[braindead101]

okay, this is what i got so far, i don't know if its right. correct me if i had a mistake

taking xaxis is // to side of funnel, and yais is perpendicular to side of funnel, i drew fbd and the forces i got are
x components : Fs, - mg cos theta
y components : Fn, - mg sin theta

so i hvae two equations:
Fs - mg cos theta = mw^2r (1)
Fn - mg sin theta = ma
Fn - mg sin theta = 0
Fn = mg sin theta
since mew (u) = Fs/Fn
Fs = u Fn
Fs = u mg sin theta
subbign that into equation (1)
u mg sin theta - mg cos theta = mw^2r
masses cancel
u g sin theta - g cos theta = w^2r
isolating for w:
w = sqrt [g((u sin theta + cos theta)/r)]

is that right?

 

[andrevdh]

I don't think so. Your Fs should be negative, but even more serious is that the centripetal acceleration of the cube is horizontal, pointing inwards towards the vertical axis.