NA19
- 16
- 0
Homework Statement
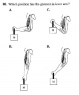
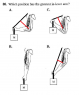
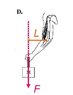
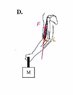
The diagram is attached. It is asking which position has the greatest lever arm.
Homework Equations
The Attempt at a Solution
So, I know that the elbow is the fulcrum but what I'm struggling with is how to draw the force arrow. Where is the force coming from and where is it pointing? What is a good way to know where to draw the lever arm?