Heat and internal energy of gas

[akoma714]

One mole of an ideal diatomic gas at room temperature undergoes a transition from a to c along the diagonal path in Figure 19-23.

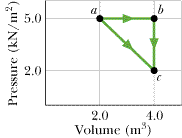
(a) During the transition, what is the change in internal energy of the gas?
-4987 J
(b) How much energy is added to the gas as heat?
____ J
(c) How much heat is required if the gas goes from a to c along the indirect path abc?
5013 J

I got part a and c right. I found the energies for path abc and added them together, because I couldn't find a way with path ac. Does the path I took matter for the heat? How do I find it using path ac?

 

[Chestermiller]

For path ac, $\Delta (PV)=nR\Delta T=-2000J$. The change in internal energy is $\Delta U=nC_v\Delta T=n\frac{5}{2}R\Delta T=\frac{5}{2}(-2000)=-5000J$

The work in going from a to c is $\int{PdV}=7000J$, so from the first law, $Q=\Delta U+W=-5000+7000=2000J$

Along path ab, the expansion is at constant pressure, so $Q=\Delta H=nC_p\delta T=n\frac{7}{2}R\Delta T=\frac{7}{2}\Delta (PV)=10000=35000J$

Along path bc, the change is at constant volume, so $Q=nC_v\Delta T=n\frac{5}{2}R\Delta T=\frac{5}{2}\Delta (PV)=\frac{5}{2}(-12000)=-30000J$

So the heat added along path abc is Q = (35000)-(30000)=5000J

So the heat added along path abc is different from that for the direct path ac. Of course, this confirms that heat added is a function of path.