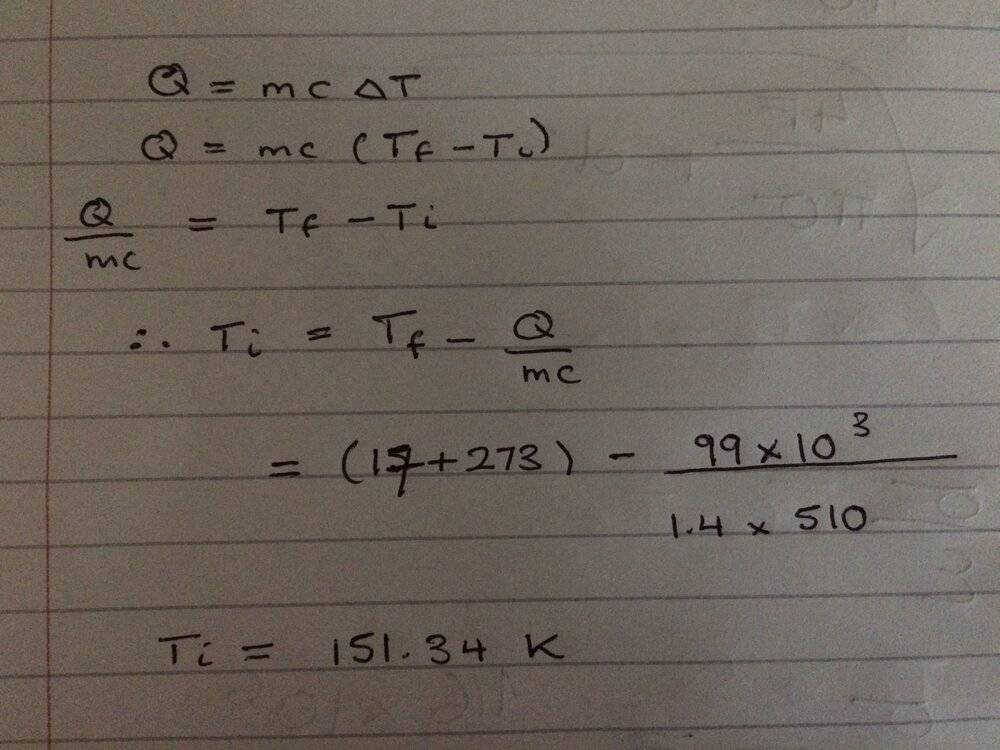SUMMARY
The discussion centers on calculating the initial temperature of a steel disk after dissipating 99 kJ of heat energy. Participants clarify that the temperature difference should be calculated using the equation Q = mcΔT, where Q is negative due to heat loss. The correct approach involves converting the final temperature of 17°C to Kelvin and adding the temperature difference derived from the heat energy dissipation. The final calculation yields an initial temperature of approximately 428.81 K.
PREREQUISITES
- Understanding of thermodynamics principles, specifically heat transfer.
- Familiarity with the equation Q = mcΔT for calculating temperature changes.
- Knowledge of unit conversions between Celsius and Kelvin.
- Basic algebra skills for manipulating equations and understanding PEMDAS/BEDMAS rules.
NEXT STEPS
- Study the principles of heat transfer in thermodynamics.
- Learn about unit conversions, particularly between Celsius and Kelvin.
- Explore common mistakes in thermodynamic calculations and how to avoid them.
- Investigate the implications of precision in scientific measurements and calculations.
USEFUL FOR
This discussion is beneficial for students studying thermodynamics, engineers working with heat transfer systems, and anyone involved in thermal analysis of materials.