godingly
- 13
- 0
1) I don't completely understands Charles Law (V = T*k) - This implies that if we increase the volume of an object, it's temperature will rise! Imagine a piston-apparatus - If we push the piston up, and increase the volume of the gas, why would its average kinetic energy rise? What would make the particles (on average) move faster?
2) I've read an example about heat, work and energy. It shows you can change a gas internal energy by either work or heat.
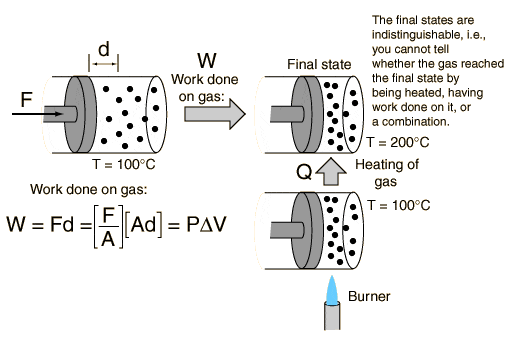
I don't understand why either of these changes will cause a rise in temperature:
a) In the work case - the gas's volume decreases, so therefore the gas's temperature should decrease as well, not increase! What's happening?
b) In the burner case - I don't understand what happens on the atomic level. I would appreciate an atomic-view explanation of what happens from when you press the burner button to the rise of the gas atoms average kinetic energy.
Thank you,
docendo discimus
2) I've read an example about heat, work and energy. It shows you can change a gas internal energy by either work or heat.
I don't understand why either of these changes will cause a rise in temperature:
a) In the work case - the gas's volume decreases, so therefore the gas's temperature should decrease as well, not increase! What's happening?
b) In the burner case - I don't understand what happens on the atomic level. I would appreciate an atomic-view explanation of what happens from when you press the burner button to the rise of the gas atoms average kinetic energy.
Thank you,
docendo discimus