- #1
earlofwessex
- 87
- 0
I should probably start by saying that I'm not too interested in the mathematics yet, I'm after conceptual understanding. I'll get the maths easy when I've got the concepts.
ok, this is what I've got so far, stop me when i get it wrong...
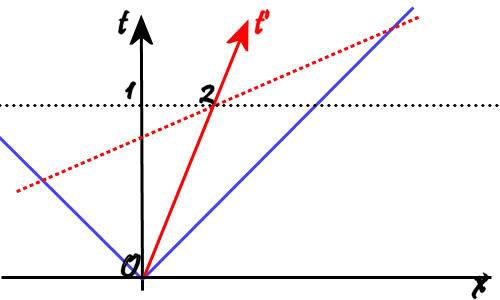
the black lines represent the inertial coordinate system (one time and one spatial axis) of an observer, who is passed at t=0 by another inertial observer (red line) traveling at velocity V wrt the coordinates. at the same instance, two photons are emmitted from the origin. these are the blue lines (c = 1).
since both observers were present at the event, both observers see the photons an equal distance from their own location, hence the dotted lines which represent constant time for each respective (colour coded) observer. (obviously the red line is parralell to the x' axis not shown) this is simultineity fallen out of the window.
its also pretty easy to get length contraction, as any distance along the x' axis will be shorter when projected onto the x axis, though I'm not sure that this is the correct understanding as it puts a limit on the contraction (1/root2 of the original length)
time dilation is however just confusing me. i can see that the "stationary" observer measures time along the vertical t axis, but is it right to say that the primed observer measures time along the t' axis? that means between 0 and 2 on the diagram the primed observer (according to the non primed observer) has experienced more time than the non primed. it looks to me like (again according to the non primed observer) the red line is longer, and a clock following this path will have ticked more often than the black line clock.
this doesn't fit what I've read so far about time dilation, so where am i going wrong? can I even use this diagram to explain time dilation?
thanks very much.
ok, this is what I've got so far, stop me when i get it wrong...
the black lines represent the inertial coordinate system (one time and one spatial axis) of an observer, who is passed at t=0 by another inertial observer (red line) traveling at velocity V wrt the coordinates. at the same instance, two photons are emmitted from the origin. these are the blue lines (c = 1).
since both observers were present at the event, both observers see the photons an equal distance from their own location, hence the dotted lines which represent constant time for each respective (colour coded) observer. (obviously the red line is parralell to the x' axis not shown) this is simultineity fallen out of the window.
its also pretty easy to get length contraction, as any distance along the x' axis will be shorter when projected onto the x axis, though I'm not sure that this is the correct understanding as it puts a limit on the contraction (1/root2 of the original length)
time dilation is however just confusing me. i can see that the "stationary" observer measures time along the vertical t axis, but is it right to say that the primed observer measures time along the t' axis? that means between 0 and 2 on the diagram the primed observer (according to the non primed observer) has experienced more time than the non primed. it looks to me like (again according to the non primed observer) the red line is longer, and a clock following this path will have ticked more often than the black line clock.
this doesn't fit what I've read so far about time dilation, so where am i going wrong? can I even use this diagram to explain time dilation?
thanks very much.