Help with a complex pulley problem

In summary, the problem involves a diagram with ideal pulleys, a massless hanging surface, and a person with mass m pulling each string with a force F. The goal is to solve for F in terms of m and g. The diagram shows that the forces on the ends are both F, but the values of T1 and T2 are unknown. To solve, the equation ƩF=0=-mg+2F+F+F+T1+T2 is used and the pulley associated with T1 is isolated and a free body diagram is drawn.
  • #1
stonecoldgen
109
0

Homework Statement


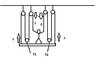
The problem is based in the diagram (the jpg attached).

All pulleys are ideal pulleys, and the hanging surface is massless. the problem states that the guy with mass m pulls each string with a force F, and asks to solve the value of F in terms of m and g. Since the pulleys are ideal I know that the forces on the ends are both F, as marked in the diagram, but I don't know what are the values of T1 and T2 (note:T1=T2). If anyone could please help I would appreciate it.

ƩF=0=-mg+2F+F+F+T1+T2
 

Attachments

  • complex pulley problem.jpg
    complex pulley problem.jpg
    16.7 KB · Views: 1,245
Physics news on Phys.org
  • #2
isolate the pulley associated with T1 and draw a free body diagram for it.
 

1. How do I determine the mechanical advantage of a complex pulley system?

The mechanical advantage of a complex pulley system can be determined by counting the number of ropes supporting the load. Each supporting rope will reduce the weight of the load by a certain amount, and the mechanical advantage is the ratio of the weight of the load to the reduced weight.

2. What is the difference between a fixed and a movable pulley in a complex pulley system?

A fixed pulley is attached to a stationary object, while a movable pulley is attached to the load and moves with it. In a complex pulley system, a fixed pulley will only change the direction of the force, while a movable pulley will also contribute to the mechanical advantage.

3. How do I calculate the tension in each rope of a complex pulley system?

The tension in each rope can be calculated by using the principle of conservation of energy. The total work done by the input force must equal the work done by the output force, and the tension in each rope can be determined using this equation.

4. Can I increase the mechanical advantage of a complex pulley system by adding more pulleys?

Yes, the mechanical advantage of a complex pulley system can be increased by adding more pulleys. However, this will also increase the distance that the rope must be pulled, and there will be more frictional forces to overcome.

5. How does friction affect the operation of a complex pulley system?

Friction can have a significant impact on the operation of a complex pulley system. It can decrease the mechanical advantage by causing energy to be lost as heat, and it can also make it more difficult to move the load. Lubricants can be used to reduce friction and improve the efficiency of the system.

Similar threads

2 pullies and 3 masses -Tension
    • Introductory Physics Homework Help
Replies
18
Views
1K
3 pulley problem with attached masses
    • Introductory Physics Homework Help
Replies
15
Views
2K
Experimental Design: Pulley and Mass Hangers
    • Introductory Physics Homework Help
Replies
30
Views
1K
Acceleration of a mass lowered by a motor (Help with Non-Ideal Pulley)
    • Introductory Physics Homework Help
Replies
4
Views
967
Pulley system to balance the weight of a person
    • Introductory Physics Homework Help
Replies
7
Views
1K
Ideal Vs Real Mass Pulley system
    • Introductory Physics Homework Help
Replies
10
Views
3K
Moment of Inertia with pulley and two masses on a string (iWTSE.org)
    • Introductory Physics Homework Help
Replies
8
Views
8K
Calculate the initial acceleration of this pulley system
    • Introductory Physics Homework Help
Replies
8
Views
2K
Motor lowers a mass over a pulley, find acceleration of mass
    • Introductory Physics Homework Help
Replies
3
Views
1K
Using Effective Mass to find the accelerations of 3 masses connected by pulleys
    • Introductory Physics Homework Help
Replies
25
Views
2K

Hot Threads

Recent Insights

Back
Top