- #1
Roy S Ramirez
- 24
- 4
Hello!
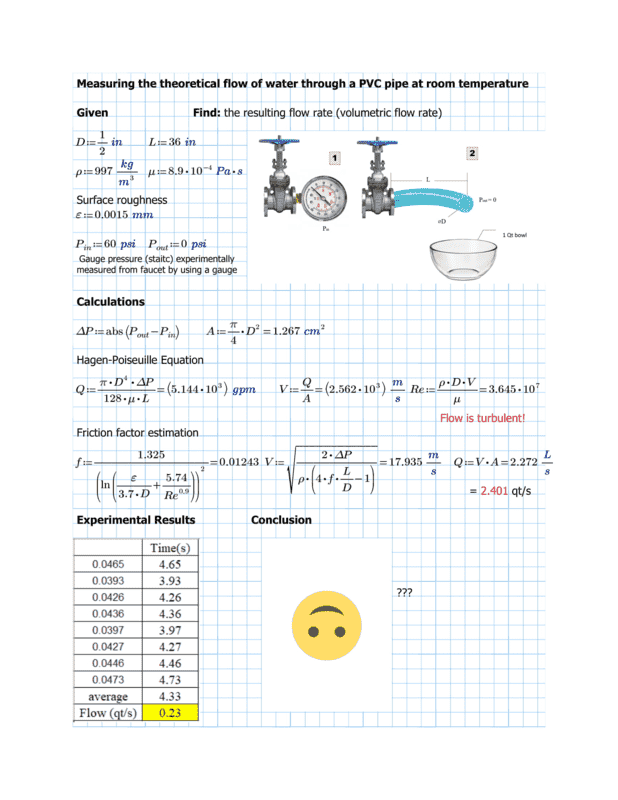
I hope you are all doing well! I've been always intrigued by fluid mechanics and decided to try out a quick experiment with my water faucet. After using some equations I found online [1] [2], I plugged a hose to the faucet and let the water run. I filled a 1 quart bowl and recorded the time it took to fill it. Without closing the valve, the experiment was repeated several times.
After comparing the experimental to theoretical results, there was a huuuge discrepancy.
Could you please help me see where the problem is? I feel like this should be a very simple problem...
ref:
[1] https://engineering.stackexchange.c...o-calculate-flow-rate-of-water-through-a-pipe
[2] https://www.lmnoeng.com/moody.php
I hope you are all doing well! I've been always intrigued by fluid mechanics and decided to try out a quick experiment with my water faucet. After using some equations I found online [1] [2], I plugged a hose to the faucet and let the water run. I filled a 1 quart bowl and recorded the time it took to fill it. Without closing the valve, the experiment was repeated several times.
After comparing the experimental to theoretical results, there was a huuuge discrepancy.
Could you please help me see where the problem is? I feel like this should be a very simple problem...
ref:
[1] https://engineering.stackexchange.c...o-calculate-flow-rate-of-water-through-a-pipe
[2] https://www.lmnoeng.com/moody.php