How Can I Solve for the Forces on Pruning Shears with Three Subsystems?

[wnvl1]

Homework Statement

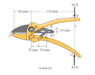
Find the forces in hinches B, C and D.

Relevant Equations

Sum forces = 0 and sum torques = 0

First subsystem:

$$C_x + F_{DE} \cos(45) = 0$$

$$C_y + F_{DE} \sin(45) + 20= 0$$

$$F_{DE} \sin(45) \times 25 + 20 \times 150= 0$$Second subsystem:

$$B_x - C_x = 0$$

$$B_y - C_y - A_y - 20= 0$$

$$-F \times 150 + A_y \times 60 - C_x \times 30 = 0$$Third subsystem:

$$-B_x - F_{DE} \cos(45) = 0$$

$$A_y -B_y - F_{DE} \sin(45)= 0$$

$$-A_y \times 60+ F_{DE} \sin(45) \times 55 = 0$$Problem is that I have 9 equations and only 6 unknwowns.

 

[TSny]

Some of your equations are redundant. For example, consider the first equation in each subsystem. These three equations are redundant.

 

[wnvl1]

Thank you, I see. It was in my mind that all equations were needed. This solves my problem.