mateomy
- 305
- 0
Working along step-by-step with a text and I'm stumped as to how they reached a conclusion. In the first picture you see two plates aligned at an unspecified angle, theta. One plate is at a potential V and the other is grounded. The distance between the plates at one end is d, and at the other end d+a. You can see in the second picture how they've set it up with respect to a two dimensional coordinate system. Maybe it's late and I'm braindead or maybe not in any even I can't see how they've formed the relationship between b,d and a to determine the distance between the actual origin and the intersection of the plates (dotted lines in picture three). Can anybody enlighten me?
Thanks.
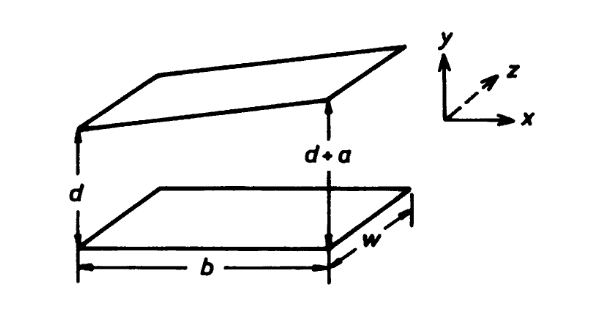
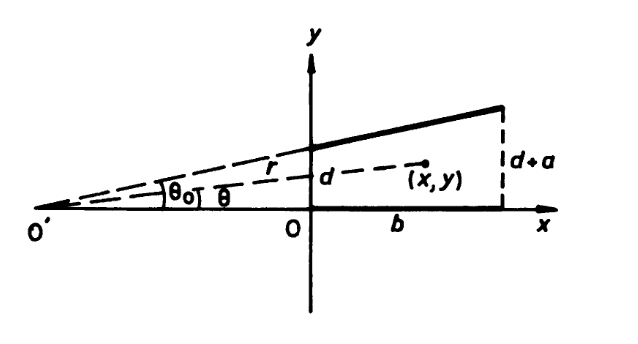
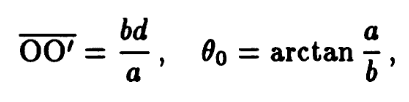
Thanks.