HeLLz aNgeL
- 30
- 0
Homework Statement
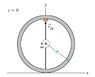
You are to find the coordinates of a pebble stuck in the tread of a rolling tire that is rotating counterclockwise (i.e., in the positive sense) with angular velocity omega. The tire rolls without slipping on the ground (which is at y = 0 ). The outer radius of the tire is R. At time t = 0 , the pebble is at the top of the tire, as shown.
a). Find the velocity of the axle of the tire relative to a fixed point on the ground, v_vec_ag(t). Note the order of the subscripts: velocity of axle measured relative to the ground. Express your answer in terms of R, omega, and x_unit and/or y_unit.
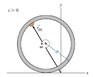
The pebble and tire have now rolled as shown in the figure. View Figure Answer the following questions for t>0.
b). Find the position vector of the pebble relative to the initial point of contact between the wheel and ground at a time t, r_pg_vec(t).
Express the position vector of the pebble in terms of R, omega, t, and the unit vectors x_unit and/or y_unit of the xy coordinate system shown.
c). Find v_vec_pg(t), the velocity vector of the pebble with respect to a fixed point on the ground, in terms of the unit vectors x_unit and y_unit of the xy coordinate system shown.
Express the velocity vector in terms of R, omega, t, and x_unit and/or y_unit.
d) Now find a_vec_pg(t), the acceleration vector of the pebble with respect to a fixed point on the ground.
Express your answer in terms of R, omega, t and x_unit and/or y_unit of the xy coordinate system shown.
The Attempt at a Solution
ok, for the first one, i know v = rw, but how do i write it in terms of vectors, v =rwx ?
and for part b, i have no clue how i should be approaching this ... just seems too weird :S