How Do You Calculate Velocities from a Potential-Energy Diagram?

[fsm]

I am given a potential-energy diagram with the vertical axis is potential-energy and the horizontal axis is x. The mass of the particle is 500g.

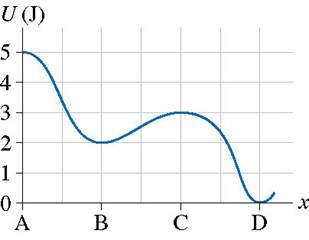
They are asking the velocities of b, c, and d. I am completely lost. I can't even find an example in the book. This isn't good :(

 

[berkeman]

The Homework Posting Template asks you to list what equations and principles apply to your problem. What can you say about changes in PE? What is the PE of a mass that is raised some height against the force of gravity?

 

[turdferguson]

If its not potential then what is it?

 

[berkeman]

If what's not potential?

There are several different sources of PE, right? It can come from compression of a spring, or storing compressed air, or the form that I think the OP problem is referring to. But without the exact problem statement and context, it's hard to say.

fsm -- can you please post the exact text of the question, and maybe say what you are studying at the moment. And then offer some ideas about how to solve the problem.

 

[NTUENG]

Hi fsm,

U need to know how to interpret graphs and the conservation of mechanical energy to do this. Ok, initially, the total energy of the particle is 5J. At point B, it has lost some P.E. and what's left is 2J. Some of the P.E. has been converted into K.E. which is 3J. U know the mass of the particle (500g). U can use the equation K.E. = 1/2 mv² and solve for v. Do the same for points C and D. U should get the answers pretty fast.

Hope that helps.

 

[berkeman]

Hi fsm,

U need to know how to interpret graphs and the conservation of mechanical energy to do this. Ok, initially, the total energy of the particle is 5J. At point B, it has lost some P.E. and what's left is 2J. Some of the P.E. has been converted into K.E. which is 3J. U know the mass of the particle (500g). U can use the equation K.E. = 1/2 mv² and solve for v. Do the same for points C and D. U should get the answers pretty fast.

Hope that helps.

Except, what if it's a ball rolling down an incline without slipping -- how does that change the velocity answer? And what would be different if it were a cylinder instead of a ball? We aren't given enough information by the OP to just say use 1/2mv^2.