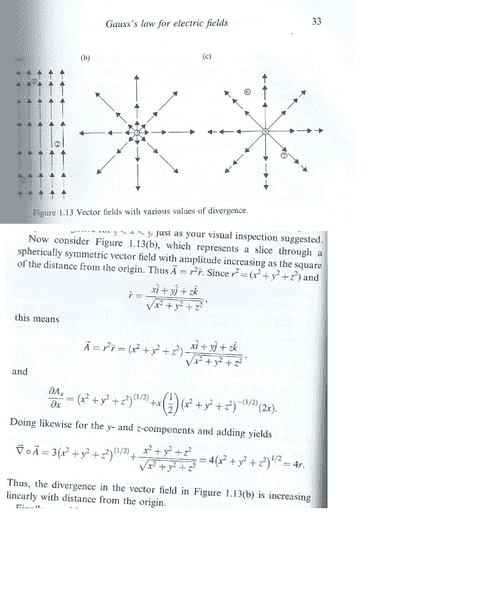How Do You Take Derivatives in Gauss's Law for Electric Fields?

[astrobird]

I'm reading a book that deals with Gauss's law for electric fields in its differential form. I'm stuck now on a page that discusses taking deriviatives of the equation for a vector field:
→
A

I'm familiar with the rules for deriviatives of products and quotients but unfortunately I cannot follow the steps that are being done in this case.
Would someone here be able to add a bit of extra info to what the page explains? Or refer me to a resource that explains the same principles but with more intermediate steps?

Here is the relevant part of the page which I scanned:

 

[Hertz]

The math in this screenshot here is vector calculus from Calc III.

Imagine those vector fields drawn on an x-y plane, where x is the horizontal, y is the vertical, and the origin of the plane is at the center of the vector fields.

I'm not sure how much you know about vector fields, so I'm going to give a quick explanation of them. As you should know, vectors have a magnitude and direction. You can also have a "vector field" where there is a vector associated with every point on the x-y plane. Here is an example of such a vector field:

$\vec{F}(x, y)=1\hat{i}+2\hat{j}$

A vector that is magnitude 1 is called a "unit vector" and is represented with a "hat" over it rather than an arrow. The two unit vectors in my above example are i and j. The "i hat" vector is length 1 and ALWAYS points in the direction of positive x. The "j hat" vector is similar, but it always points in the direction of positive y. As you can see, you can multiply a unit vector by something to make it have a bigger magnitude, or you can add unit vectors together to get a vector that points in any direction. Anyways, without further ado, I'll move on to what you posted..

They give you a definition of the r hat vector. It looks complicated, but really it's not. The r hat vector is the unit vector that always points directly outward from the origin. As you can see in example b and c, the r hat vector would be useful in explaining this vector field. (While the j hat vector would be useful for explaining example a.)

With the definition of the r hat unit vector, you can specify the vector field in example b as follows:

$\vec{A}=r^2\hat{r}$
"Vector field A always points away from the origin and has a magnitude of r^2"

Also, if you explicitly write out the r hat unit vector, you can separate it into i hat, j hat, and k hat terms. (k hat is the unit vector that points in the direction of positive z axis.) This means that you could theoretically take the dot product with another vector right? Well, that is what they are doing. They are saying, "take the vector field in example three and take the dot product with another vector." The other vector that they are talking about is called the Del Operator.

$\vec{∇}=\frac{\partial}{\partial x}\hat{i}+\frac{\partial}{\partial y}\hat{j}+\frac{\partial}{\partial z}\hat{k}$

I'm assuming you know how to take a dot product.
As you can see, if you take the dot product with this vector and some other vector field like the ones in the example, you will have to take some derivatives. Anyways, that's not the important part. That is technical calc III stuff. The point is that they are calculating something known as "Divergence" which is basically how much the vector field is "exploding outward".

As you can see, example b and c have divergence. Example b diverges more as you get further away from the origin. Example c diverges less as you get further away from the origin, etc.

*****

Summary:
They are finding the divergence of example b.
To do this, they take the dot product between "vector field b" and "the del operator". This gives divergence.
They then see that the divergence is equal to 4r. This means that the field "diverges more" as you move further away from the center.

I hope this helped. This stuff can be quite complicated, but in my honest opinion, it's the most interesting math I've ever had the pleasure of studying. Vector calculus is just plain beautiful haha

 

[astrobird]

Thank you very much for the fast and elaborate reply! Your explanation is really helpful and I think I understand it much better already.

The one thing that I don't get yet is how they go from the formula for
$\vec{A}$
to the derivative shown below that.
I have tried to take the derivative myself on a piece of paper but when I apply the rules for derivatives of products and quotients I don't arrive at the same result. For example, based on the rules for derivatives of quotients I was expecting to have a part with a minus sign in front of it in the derivative but there is none in the derivative shown in the book.

Do you think I'm doing something wrong with applying the rules for derivatives of products and quotients or are there additional rules involved here because it concerns the derivative for the formula of a vector field? If the latter is the case, then I guess I don't know the rules and then it makes sense that I don't arrive at the correct result.
I have been searching online just now to find some info on this but I'm having a hard time finding some examples from Calc III that are similar to what is done in the book.

 

[Hertz]

Remember, they are not taking "the derivative of the vector field", they are taking the dot product of the vector field and the del operator. I know I can be redundant, but for the sake of being clear, this is called "the divergence" of the vector field, not "the derivative" of it.

This means that instead of taking d/dx of the entire vector field, they only take d/dx of the i hat component. Or in other words, they only take d/dx in the x direction. They don't care about d/dx in the other directions.

Example:

$\vec{F}(x, y)=x\hat{i}+y\hat{j}$

$\vec{∇}\bullet\vec{F}(x, y)=\frac{\partial}{\partial x}(x)+\frac{\partial}{\partial y}(y)=2=Div(\vec{F})$

In the example they use, they are only doing the "x-part" of the dot product. A little bit lower, they do the full dot product but they don't really show their work, they just give you the simplified answer.

I hope I understood your question right :)

-edit
For the record. I just took d/dx of the x component and got the same thing they did.

HINT:
The x component of the vector field is $x\sqrt{x^2+y^2+z^2}$

 

[astrobird]

Remember, they are not taking "the derivative of the vector field", they are taking the dot product of the vector field and the del operator.

Thanks that was helpful, I didnt really get that part, and in a way I still wonder if I now get it (see below)

Your HINT mentioning the x component of the vector field is also really helpful. Based on that x component you mention I also arrive at the same derivative as they did and also the step below (the full dot product) follows naturally from that, I also get the same result for that.

The only thing that I still don't get is how you obtained the x component of the vector field that you mention in your hint:
χ$\sqrt{x^{2}+y^{2}+z^{2}}$
I don't see how that follows from the formula for
$\vec{A}$

I have a feeling I'm missing something that it pretty obvious to others, one more hint?

I have a book on Engineering mathematics by K.A stroud which I'm currently also studying, thing is that I'm through only one third of the book, I guess all this stuff will come more natural to me once I have worked through the full book

 

[Hertz]

You should rely on study of math for this type of thing, not study of engineering. You should understand the math before attempting to make use of it in the physical world.

Anyways, this should help you:

$\vec{A}=r^2\hat{r}$

$\vec{A}=(x^2+y^2+z^2)\hat{r}$

$\vec{A}=(x^2+y^2+z^2)\frac{x\hat{i}+y\hat{j}+z\hat{k}}{\sqrt{x^2+y^2+z^2}}$

$\vec{A}=\sqrt{x^2+y^2+z^2}(x\hat{i}+y\hat{j}+z\hat{k})$

$\vec{A}=x\sqrt{x^2+y^2+z^2}\hat{i}+y\sqrt{x^2+y^2+z^2}\hat{j}+z\sqrt{x^2+y^2+z^2}\hat{k}$

You can now see that the "x component" of the vector field is $x\sqrt{x^2+y^2+z^2}$ because that is the part that corresponds with the i hat vector. Remember, the i hat vector means "in the direction of positive x axis".

edit-
It's important to remember that this is a pretty complicated example of a vector field. Not only is it 3D, but it is radial so it includes r hat, which obviously makes it more complicated.

If I were you, I would get some paper and a pencil and just mess around with vector fields. Come up with some random simple 2D vector fields and see if you can draw them. Here's some examples:

$\vec{F}=x\hat{i}+y\hat{j}$

$\vec{F}=y\hat{i}-x\hat{j}$

What's the difference between these two fields? What is their divergence? There are limitless possibilities to the types of vector fields you can come up with. I would say working with some simpler ones first would make the entire process easier.

You might also want to purchase a calculus book and read the vector calculus chapter. Or look up some vector calculus videos online. Trying to understand Gauss's Law and stuff like that before having a background in vector calculus can be nearly impossible. Those types of things are even hard to understand when you have a good understanding of vector calculus..

 

[astrobird]

Thanks again, your steps are very clear and I do understand now how we get the x component. I also realize now that you are right when saying that I should understand the basic math behind this all better before attempting to fully understand Gauss's Law and similar stuff.

I will be reading more about 2D vector fields and experiment with indeed some simple examples, sounds like a good plan, thanks for all the help!