Thrax
- 23
- 0
Hi,
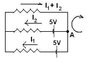
I’m having some trouble with Kirchhoff's circuit law problems regarding two batteries in the circuit. I've attached a crude picture of a problem i picked to understand what's going on.
So for the bottom loop I have
5V - 5v = i1 - i2
0= i1 – i2
The top loop I’m coming up with
5 = i2 -2(i1+i2)
5= i2 -2i1 -2i2
-1(5 = -2i1 -i2)
So I’m left with
5 =2i1 +i2
0= i1 – i2
5=-2i1
0=- i1
5=-3i1
5/-3 = i1
But, I think this is wrong.
I’m having some trouble with Kirchhoff's circuit law problems regarding two batteries in the circuit. I've attached a crude picture of a problem i picked to understand what's going on.
So for the bottom loop I have
5V - 5v = i1 - i2
0= i1 – i2
The top loop I’m coming up with
5 = i2 -2(i1+i2)
5= i2 -2i1 -2i2
-1(5 = -2i1 -i2)
So I’m left with
5 =2i1 +i2
0= i1 – i2
5=-2i1
0=- i1
5=-3i1
5/-3 = i1
But, I think this is wrong.