How is Max Power Transferred in a Circuit?

  • Thread starter utkarshakash
  • Start date
  • Tags
    Max Power
In summary, the conversation discusses finding the maximum power transferred through a circuit given a specific Norton's equivalent resistance. The solution involves finding the Norton's current and applying Kirchhoff's law. The maximum power is transferred to a load equal to the internal resistance of the generator, and this information helps to solve the problem.
  • #1
utkarshakash
Gold Member
854
13

Homework Statement


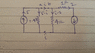
Find the max power transferred through R in the circuit given.


Homework Equations



See attachment for the diagrams

The Attempt at a Solution



The Norton's equivalent resistance is 5.4Ω. For finding the Norton's current, I need to find the short-circuit current through the terminal AB.
Applying Kirchhoff's law to the middle loop, I can write
4(i-2)=1.43(5-i)
i=2.79

Thus, P = Inorton2Req = 42.04.
But this is the incorrect answer.
 

Attachments

  • elec_1.gif
    elec_1.gif
    124 KB · Views: 579
  • elec_2.gif
    elec_2.gif
    103.7 KB · Views: 526
Physics news on Phys.org
  • #2
The maximum power is transferred to a load equal to the internal resistance of the generator. You calculated the power supplied to the Norton resistance, if there was no load. How much current would flow through the loading resistance R if R=Req?

ehild
 
  • #3
ehild said:
The maximum power is transferred to a load equal to the internal resistance of the generator. You calculated the power supplied to the Norton resistance, if there was no load. How much current would flow through the loading resistance R if R=Req?

ehild

Thanks! It solved my problem.
 

Related to How is Max Power Transferred in a Circuit?

1)

What is the maximum power that can be generated by a specific energy source?

The maximum power generated by an energy source depends on several factors such as the type and efficiency of the technology used, environmental conditions, and operational constraints. It can be calculated by determining the maximum theoretical output of the energy source and factoring in these variables.

2)

How do you determine the maximum power output of a renewable energy system?

The maximum power output of a renewable energy system can be determined by conducting a site assessment to analyze the available resources (e.g. sunlight, wind, water) and using mathematical models to simulate the expected power output based on these resources and the technology used.

3)

What is the difference between peak power and average power in an energy system?

Peak power refers to the maximum power output that a system can achieve at any given moment, while average power is the average amount of power that is generated over a certain period of time. Peak power is useful for understanding the maximum capabilities of a system, while average power provides a more realistic picture of the system's overall performance.

4)

How can the maximum power generated by a system be increased?

The maximum power generated by a system can be increased by improving the technology used, optimizing the system's design and operation, and utilizing energy storage solutions. Additionally, incorporating multiple energy sources and using smart control systems can also help maximize the power output of a system.

5)

Is it possible to accurately predict the maximum power output of a system?

While it is possible to estimate the maximum power output of a system using mathematical models and simulations, the actual power output may vary due to unpredictable factors such as weather conditions and equipment failures. Regular maintenance and monitoring can help ensure that the system is operating at its maximum potential.

Similar threads

How can I get steady state of complicated heat transfer problem?
Replies
1
Views
900
Power dissipated in this circuit with 2 batteries and 3 resistors
Replies
22
Views
3K
Find frequency such that two components have same average power
Replies
4
Views
1K
Differential Amplifier Common Mode Thevenin Equivalent
Replies
1
Views
1K
Two networks described by v-i graph: Find voltages when interconnected
Replies
1
Views
680
I An attempt to understand the associated variable conventions in circuits
Replies
1
Views
1K
NPN transistor overheating even when used with appropriate parameters
Replies
11
Views
2K
Max power of a photovoltaic cell -- where did I go wrong?
Replies
4
Views
1K
Understanding example in Wikipedia entry for open circuit voltage
Replies
3
Views
920
Worst-case power consumed by a circuit with MOSFETs
Replies
2
Views
536

Hot Threads

Recent Insights

Back
Top