lakmalp
- 26
- 0
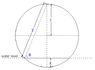
A hollow cylinder (but not open ended) is allowed to float on a liquid. Can anyone please help me how to calculate the height (h) it submerge? I want to get a relationship between height and cylinder weight.
I can calculate the volume of submerged part. But no idea how to derive a formula with weight and height.
I can calculate the volume of submerged part. But no idea how to derive a formula with weight and height.