How to calculate the ratio of weight?

  • Thread starter Thread starter asteorit
  • Start date Start date
  • Tags Tags
    Ratio Weight
AI Thread Summary
To calculate the ratio of weights for two bodies connected by linear actuators, the forces acting on each body must be analyzed using Newton's second law (F=ma). The bodies move apart under the influence of a force F, with friction considered, and their movements are defined by their respective equations of motion. The key is to establish the relationship between the masses (m1 and m2) based on the total distance L they travel, which is the sum of their individual distances. The discussion emphasizes the need to derive the mass ratio from the equations of motion while considering the forces acting on each body. Understanding this relationship is crucial for determining the mass ratio when the total distance traveled is fixed.
asteorit
Messages
15
Reaction score
0

Homework Statement


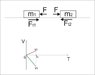
Two body move apart by force. Frictional forces are considering. How to calculate the ratio of weight?
m1<m2
Ft1=k*g*m1
Ft2=k*g*m2

Homework Equations


v1(t1)=\frac{F_{t1}-F}{m_{1}}*t_{1}
x1(t1)=\frac{F_{t1}-F}{m_{1}}*\frac{t^{2}_{1}}{2}

v2(t1)=\frac{F-F_{t2}}{m_{2}}*t_{1}
x2(t1)=\frac{F-F_{t2}}{m_{2}}*\frac{t^{2}_{1}}{2}

What is the procedure of calculation.
Thank you for your help.
 

Attachments

  • Grafika2.jpg
    Grafika2.jpg
    15.2 KB · Views: 526
Physics news on Phys.org
welcome to pf!

hi asteorit! welcome to pf! :smile:

sorry, but i don't understand the set-up :redface:

what is the connection between these two bodies?
 


tiny-tim said:
hi asteorit! welcome to pf! :smile:

sorry, but i don't understand the set-up :redface:

what is the connection between these two bodies?

Hi tiny-tim,

These two bodies are connected by linear actuators. Force F of the linear actuator, will act on both the bodies. We know that the bodies should move along the path L, L=x1(t1)+x2(t1). We know that m1<m2.
If I assume correctly, and the trajectory of bodies depends on the mass ratio. Or is also dependent on the time t1?
What is the ratio of the mass of bodies\frac{m_{2}}{m_{1}}=?, if the sum of their orbits must be equal to L?
 
hi asteorit! :wink:

i see … so it's equal-and-opposite-reaction-forces, but without contact

ok, then start by writing out Ftotal = ma for each body …

what do you get? :smile:​
 
tiny-tim said:
hi asteorit! :wink:

i see … so it's equal-and-opposite-reaction-forces, but without contact

ok, then start by writing out Ftotal = ma for each body …

what do you get? :smile:​

I do not understand it, to me you ask? Some will not understand it?
Because I need to know what is the ratio of the masses.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Tension in a string connecting two blocks having equal and opposite velocities
Replies
21
Views
308
Experimental Design: Pulley and Mass Hangers
Replies
30
Views
3K
Solving for Masses in an Atwood Machine
Replies
8
Views
2K
Ratio of volumes in a vertical cylinder with a piston
Replies
3
Views
700
Finding the magnitude of the force
Replies
3
Views
2K
3 pulley problem with attached masses
Replies
15
Views
5K
How to calculate velocity of infinite-stage rocket?
Replies
2
Views
1K
Find the height of a lamp based on the velocities of projectiles
Replies
40
Views
2K
Calculating tensions and acceleration
Replies
10
Views
2K
Two bodies connected with an elastic thread moving with friction
Replies
6
Views
1K

Hot Threads

Recent Insights

Back
Top