Rachel_S
- 1
- 0
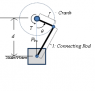
As shown in this picture, if Fb, l (length of connecting rod), r (radius of crank) and θ is given, how to calculate the torque the slider crank?
I know it can be a simple question for Mechanical Engineering majors, but I am an Electrical Engineering major and have very little knowledge in Mechanical Engineering. I am working on a project related to slider crank systems and really need to know this. It would be great if you could tell me which book introduces slider crank torque calculation too.
Thanks!
I know it can be a simple question for Mechanical Engineering majors, but I am an Electrical Engineering major and have very little knowledge in Mechanical Engineering. I am working on a project related to slider crank systems and really need to know this. It would be great if you could tell me which book introduces slider crank torque calculation too.
Thanks!