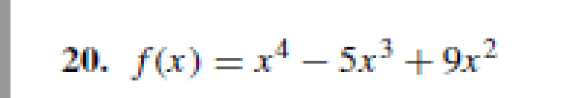That is the fourth step. Start with step one, two and three!
We start with step one - differentiation:
\begin{align*}
f(x)&=x^4-5x^3+9x^2=x^2(x^2-5x+9)\\
f'(x)&=4x^3-15x^2+18x=x(4x^2-15x+18)\\
f''(x)&=12x^2-30x+18=6(x-1)(2x-3)
\end{align*}
Step two - zeros:
I do not know which method you use to determine whether a quadratic function has real solutions or not. In this case, both quadratic terms are positive:
\begin{align*}
x^2-5x+9 &> 0\text{ for all }x\in \mathbb{R}\\
4x^2-15x+18&>0\text{ for all }x\in \mathbb{R}
\end{align*}
This means that everything of interest happens at ##x=0## as the only zero of ##f(x)## and ##f'(x)##. However, there is a change in curvature, between right to left curve or the other way around. We will see later. For now,
$$
f''(x)=0 \Longrightarrow x=1 \text{ or }x=1.5
$$
But we still have step three - asymptotic behaviour:
\begin{align*}
\displaystyle{\lim_{n \to \infty}}f(n)&= +\infty \\
\displaystyle{\lim_{n \to -\infty}}f(n)&=+\infty
\end{align*}
This means, so far we have
View attachment 326451
and something interesting going on at ##x=1## and ##x=1.5.##
Now, investigate what happens at ##f(0)=0.## How does the function behave left and right of it?
If you have done this, then we consider what happens to the curvature, which is ##f''(x),## to the left of ##x=1,## between ##1<x<1.5## and to the right of ##x=1.5.##