Ari
- 3
- 0
1. Homework Statement
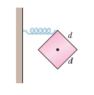
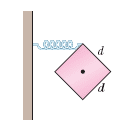
The 4.00 kg cube in the figure has edge lengths d = 8.00 cm and is mounted on an axle through its center. A spring ( k = 1400 N/m ) connects the cube's upper corner to a rigid wall. Initially the spring is at its rest length. If the cube is rotated 4.00° and released, what is the period of the resulting SHM?
m = 4 kg
d = .08 m
k = 1400 N/m
Θ = 4°
T = ?
2. Homework Equations
I = (1/6)Md2
F = ma
F = -kx = -(mω2x)
k = mω2
τ = -d(FgsinΘ)
3. The Attempt at a Solution
Restoring force is:
F = -kx while x = dsinΘ so...
F = -kdsinΘ
F = -(1400)(.08)sin(4°)
F = -7.8127 N
Newton's 2nd Law gives:
F = ma = F/m
a = (-7.8127)/4 = -1.9532
Using k = mω:
k = mω
ω = k/m = 1400/4 = 350
Using F = -kx:
x = F/-k
x = (-7.8127)/(-1400) = .00558 m
Restoring torque is:
τ = -dmgsinΘ while τ = Iα so...
Iα = -dmgsinΘ
α = -(.08)(4)(9.81)sin(4°) = -.219
Rotational to linear:
a = αr , r = .1131 m
a = -.0248
I'm not sure where to go with this further, and to be honest, not even sure if I'm going in the right direction.
Another thing is I'm not sure whether I'm supposed to use T = 2π √(m/k) or another equation, since that equation is for SHM of springs, but I can't seem to get anywhere with it.
The 4.00 kg cube in the figure has edge lengths d = 8.00 cm and is mounted on an axle through its center. A spring ( k = 1400 N/m ) connects the cube's upper corner to a rigid wall. Initially the spring is at its rest length. If the cube is rotated 4.00° and released, what is the period of the resulting SHM?
m = 4 kg
d = .08 m
k = 1400 N/m
Θ = 4°
T = ?
2. Homework Equations
I = (1/6)Md2
F = ma
F = -kx = -(mω2x)
k = mω2
τ = -d(FgsinΘ)
3. The Attempt at a Solution
Restoring force is:
F = -kx while x = dsinΘ so...
F = -kdsinΘ
F = -(1400)(.08)sin(4°)
F = -7.8127 N
Newton's 2nd Law gives:
F = ma = F/m
a = (-7.8127)/4 = -1.9532
Using k = mω:
k = mω
ω = k/m = 1400/4 = 350
Using F = -kx:
x = F/-k
x = (-7.8127)/(-1400) = .00558 m
Restoring torque is:
τ = -dmgsinΘ while τ = Iα so...
Iα = -dmgsinΘ
α = -(.08)(4)(9.81)sin(4°) = -.219
Rotational to linear:
a = αr , r = .1131 m
a = -.0248
I'm not sure where to go with this further, and to be honest, not even sure if I'm going in the right direction.
Another thing is I'm not sure whether I'm supposed to use T = 2π √(m/k) or another equation, since that equation is for SHM of springs, but I can't seem to get anywhere with it.