How to know the direction of friction?

[jofree87]

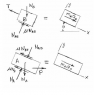
For the problem here, I am given the kinetic friction of the blocks, and I am suppose to find the acceleration of the blocks. I set the x-axis along the incline with x-positive directed towards the right, and I set both the resultant forces of of A and B down the incline since I don't which one goes up or down. Now since A and B will move in opposite directions, how do I know which way to set the frictions?

Here is a diagram of the problem, and a solution I found online,

They also set the resultant forces in the same direction but they set the frictions in different directions.

 

[kuruman]

Is the free body diagram yours or what you found on the web? Setting the resultant forces on each mass (and hence their accelerations) in the same direction provides an inconsistent picture. Look at the rope connecting the masses. It has fixed length. If mass A is accelerating down the incline (positive x-direction) the bottom part of the rope connected to mass A will get longer. This means that the top part connected to mass B will get shorter which in turn means that the acceleration of mass B is in the negative x-direction. The diagram shows both accelerations in the same direction which is inconsistent.

 

[jofree87]

Is the free body diagram yours or what you found on the web? Setting the resultant forces on each mass (and hence their accelerations) in the same direction provides an inconsistent picture. Look at the rope connecting the masses. It has fixed length. If mass A is accelerating down the incline (positive x-direction) the bottom part of the rope connected to mass A will get longer. This means that the top part connected to mass B will get shorter which in turn means that the acceleration of mass B is in the negative x-direction. The diagram shows both accelerations in the same direction which is inconsistent.

I found the diagram online but I set the resultant forces in the same manner.

I did this because I don't know exactly which block goes up or down. If I work out the problem correctly, then one of the accelerations should end up being negative. But my question is how do I know which way the frictions will go? Can I set them in any direction like how I did with the resultant forces so that it will work out in the end?

 

[kuruman]

No you cannot set the frictions in any direction you want. You have to know which way they are for the free body diagram to work. It is a good bet that the bottom block is moving down the incline, in the same direction as the component of the pulling force P along the incline. This would not be the case if the system were moving uphill after being given some initial velocity uphill and before it slides back down again. Are there words in the statement of the problem that say this is the case? If no, then assume that the bottom block is moving downhill.