HY 607: Finding the Angle for Resultant Force of Two Forces

  • Thread starter Thread starter lektor
  • Start date Start date
  • Tags Tags
    Diagram Forces
AI Thread Summary
To determine the angle for the 800N force so that the resultant force equals 2000N, the i,j method is applied. The equations used are Fi = 800sin(θ) and Fj = 1400 + 800cos(θ), leading to the relationship 2000^2 = (800sin(θ))^2 + (1400 + 800cos(θ))^2. The discussion highlights the need to simplify this equation to solve for cos(θ). Ultimately, the goal is to isolate cos(θ) to find the required angle for the resultant force.
lektor
Messages
56
Reaction score
0
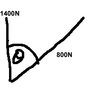
with reference to the diagram, at what angle must the 800N force be applied in order that the resultant R of the two forces has a magnitude of 2000N.

We were instructed to use the i,j method.

So, the forces for Fi = 800sin(-) and Fj = 1400 + 800 cos(-) and the resultant is 2000N.

This is where i get stuck, a^2 + b^2 = c^2
so 2000^2 = (800 sin(-))^2 + (1400+800 cos(-))^2

any help would be great.
 

Attachments

  • pic.jpg
    pic.jpg
    4.1 KB · Views: 489
Physics news on Phys.org
bump^

please help :p
 
lektor said:
bump^

please help :p

We can't see the attachment yet...
 
it is simply a diagram showing

|.../
|.../
|(-)./
|.../
|./

with the verticle line saying 1400N and the diagonal line saying 800N
 
It appears correct, expand

2000^2= 800^2 sin^2(@) + 1400^2 +2*1400*800*cos@ + 800^2*cos^2@

2000^2 - 800^2 - 1400^2 = 2*1400*800*cos@

solve for cos@


MP
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Statics problem on the resolution of forces
Replies
18
Views
2K
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
996
Find the Retarding Force due to Eddy Currents
Replies
5
Views
1K
Find moment arm of resultant force of two forces applied at two points
Replies
3
Views
1K
Forces and laws of motion -- Big gorilla hanging from two vines
Replies
3
Views
2K
To find the resultant of forces on a lamina
Replies
5
Views
3K
To find the magnitude of the resultant of forces around a triangle
Replies
4
Views
2K
Finding Resultant Force Using Cosine and Sine Law
Replies
2
Views
7K
To find the angle between the ground and rods in limiting friction
Replies
5
Views
2K
The Relationship Between Masses and Angles in a Pulley System
Replies
29
Views
3K

Hot Threads

Recent Insights

Back
Top