I have a diffcult question about torque -- me

[garylau]

Homework Statement

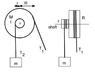
The sketch shows, from two views, a simple pulley system for raising large masses. A light, inextensible cord attached to a mass m is wound, without slipping, on a cylinder of radius r. Rigidly joined to this cylinder and mounted on the same central shaft is a cylinder of radius R. The friction between the cylinders and the shaft is negligible. The two cylinders together have mass M, moment of inertia, I and radius of gyration k. Around the larger cylinder is wound, without slipping, anther light, inextensible cord, as shown. An operator pulls with tension T1 on this cord to raise the mass m.The mass m accelerates upwards with vertical acceleration a. (i) Using Newton's laws or otherwise, write an expression for T2, the tension in the cord attached to mass m, in terms of m, g and a. (ii) Using Newton's laws for rotation or otherwise, derive an expression for the angular acceleration, α, of the cylinders, in terms of variables given in the diagram. (iii) Showing all working, derive an expression for the acceleration a of mass m in terms of some or all of the parameters T1, m, M, I, r, R and the gravitational acceleration g.

Homework Equations

F=mg
Torque=maR=I*alpha

The Attempt at a Solution

i have done my work in the paper but i found the answer get wrong in(iii)and i don't know whether it is correct or not

can i write the answer like this?

the correct answer is a =( RT1 – rmg)/( I/r + rm)

but my answer is something like...(I/r-rm)...

Do i do it wrong?thank you

 

[haruspex]

Your signs are inconsistent. You have taken α as positive anticlockwise, then written a=αr. That makes a positive down.

 

[garylau]

Your signs are inconsistent. You have taken α as positive anticlockwise, then written a=αr. That makes a positive down.

oh i see
thank
But how to make the sign of the torque and the sign of the net force consistent in general?

 

[haruspex]

oh i see
thank
But how to make the sign of the torque and the sign of the net force consistent in general?

If not using vectors then you just have to stop and think. If there is a horizontal force F you are taking as positive to the right and it acts a distance x above the axis then the moment Fx is positive clockwise, etc.

 

[garylau]

If not using vectors then you just have to stop and think. If there is a horizontal force F you are taking as positive to the right and it acts a distance x above the axis then the moment Fx is positive clockwise, etc.

but in convention
the anti-clockwise direction is the positive direction of the torque,right?

 

[haruspex]

but in convention
the anti-clockwise direction is the positive direction of the torque,right?

So write that the torque is -Fx.

 

[garylau]

So write that the torque is -Fx.

then horizontal force F to the right should be negative??

it seems it is contradicted with the "other sign of convention"(which usually we take right side to be positive and left side to be negative)

 

[haruspex]

then horizontal force F to the right should be negative??
)

No, you can keep right as positive for forces, displacements, velocities and accelerations. The problem is the torque arm, x.
If the force is displacement x below the axis then Fx will be positive anticlockwise, as desired. But with the force x above the axis it becomes -Fx. So, for these cases, you could define x as the displacement from the force to the axis, up being positive.
Unfortunately, this breaks down when you consider vertical forces with horizontal displacements. Now you have to make the displacement from the force to the axis positive to the left to get the right result.
So the simplest thing, in scalars, is just to figure it out each time: if a positive right force acts above the axis it gives a clockwise moment, so use -Fx.

For a more systematic solution you need to use vectors and cross products. A set of conventions arranges that the sign comes out right. Specifically:

• $\vec \tau=\vec r\times\vec F$, not the other way around
• the right hand rule

 

[garylau]

No, you can keep right as positive for forces, displacements, velocities and accelerations. The problem is the torque arm, x.
If the force is displacement x below the axis then Fx will be positive anticlockwise, as desired. But with the force x above the axis it becomes -Fx. So, for these cases, you could define x as the displacement from the force to the axis, up being positive.
Unfortunately, this breaks down when you consider vertical forces with horizontal displacements. Now you have to make the displacement from the force to the axis positive to the left to get the right result.
So the simplest thing, in scalars, is just to figure it out each time: if a positive right force acts above the axis it gives a clockwise moment, so use -Fx.

For a more systematic solution you need to use vectors and cross products. A set of conventions arranges that the sign comes out right. Specifically:

• $\vec \tau=\vec r\times\vec F$, not the other way around
• the right hand rule

So in my original problem

the sign of R/r should be negative so that i can get the correct answer?

 

[garylau]

No, you can keep right as positive for forces, displacements, velocities and accelerations. The problem is the torque arm, x.
If the force is displacement x below the axis then Fx will be positive anticlockwise, as desired. But with the force x above the axis it becomes -Fx. So, for these cases, you could define x as the displacement from the force to the axis, up being positive.
Unfortunately, this breaks down when you consider vertical forces with horizontal displacements. Now you have to make the displacement from the force to the axis positive to the left to get the right result.
So the simplest thing, in scalars, is just to figure it out each time: if a positive right force acts above the axis it gives a clockwise moment, so use -Fx.

For a more systematic solution you need to use vectors and cross products. A set of conventions arranges that the sign comes out right. Specifically:

• $\vec \tau=\vec r\times\vec F$, not the other way around
• the right hand rule

for these cases, you could define x as the displacement from the force to the axis, up being positive.

how about the vector x pointing in random direction?

 

[haruspex]

So in my original problem

the sign of R/r should be negative so that i can get the correct answer

Yes.

for these cases, you could define x as the displacement from the force to the axis, up being positive.

how about the vector x pointing in random direction?

i was not proposing you do that. I was just illustrating there is no simple way to determine it.

Using the vector approach, you would represent the first argument to the cross product (displacement from axis to force line) with your right index finger, and the second, the force, with your right middle finger. Your thumb indicates the direction of the result. This has to be combined with the convention that torques and angular motions also use a right hand thread rule. E.g. if the vector points away from you then the motion will appear clockwise.
In your example, your index finger points up, your middle finger to the right, and your thumb away from you.