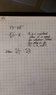ptownbro
- 60
- 0
My daughter has the following homework problem we need assistance in confirming if we've understood and completed correctly.
The Volume goes from 2.00 Liters to 7.00 Liters, the temperature changes from 800 kelvin to 150 kelvin, and the number moles of gas is quadrupled on a gas sample initially at 1.20 atm. What is the new pressure?
PV = nRT, where P = pressure, V = volume, n = moles, R = a given number at 0.0821, and T = temperature.
We assumed that since moles was used here, we need to use the "PV = nRT" version of the ideal gas equation versus the "P1V1 / T1 = P2V2 / T2" version. Given that, we also assumed we'd have to apply the factor of the changes in each applicable variable.
Volume factor = 7 / 2 = 3.5
Temperature factor = 150 / 800 = 0.1875
Moles factor = 4
Therefore, mathematically, logic stands you can apply the product of those factors to the given starting pressure amount of 1.20 atm to get the new pressure amount.
PV = nRT
P = nRT / V
P = [ (4 n) x (0.0821) x (0.1875 T) ] / (3.5 V)
P = [ (4 x 0.0821 x 0.1875) / 3.5 ] x (nT / V)
P = 0.0176 nT / V
Your factor is therefore 0.0176 which can be applied to the original pressure to get your new pressure.
Answer:
P = 1.2 atm x 0.0176
P = 0.0211 atm
Can you please confirm if our logic and answer is correct and if not where we went wrong?
Thanks!
Homework Statement
The Volume goes from 2.00 Liters to 7.00 Liters, the temperature changes from 800 kelvin to 150 kelvin, and the number moles of gas is quadrupled on a gas sample initially at 1.20 atm. What is the new pressure?
Homework Equations
PV = nRT, where P = pressure, V = volume, n = moles, R = a given number at 0.0821, and T = temperature.
The Attempt at a Solution
We assumed that since moles was used here, we need to use the "PV = nRT" version of the ideal gas equation versus the "P1V1 / T1 = P2V2 / T2" version. Given that, we also assumed we'd have to apply the factor of the changes in each applicable variable.
Volume factor = 7 / 2 = 3.5
Temperature factor = 150 / 800 = 0.1875
Moles factor = 4
Therefore, mathematically, logic stands you can apply the product of those factors to the given starting pressure amount of 1.20 atm to get the new pressure amount.
PV = nRT
P = nRT / V
P = [ (4 n) x (0.0821) x (0.1875 T) ] / (3.5 V)
P = [ (4 x 0.0821 x 0.1875) / 3.5 ] x (nT / V)
P = 0.0176 nT / V
Your factor is therefore 0.0176 which can be applied to the original pressure to get your new pressure.
Answer:
P = 1.2 atm x 0.0176
P = 0.0211 atm
Can you please confirm if our logic and answer is correct and if not where we went wrong?
Thanks!