member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this,
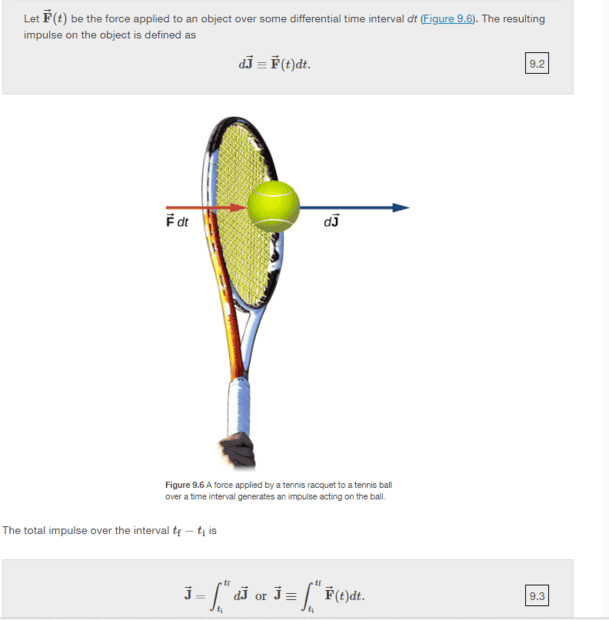
Can someone please tell me why they integrate the impulse over from ##t_i## to ##t_f##? Why not from ##j_i## to ##j_f##? It seems strange integrating impulse with respect to time.
Many thanks!
Can someone please tell me why they integrate the impulse over from ##t_i## to ##t_f##? Why not from ##j_i## to ##j_f##? It seems strange integrating impulse with respect to time.
Many thanks!