kevtimc25
- 5
- 0
Hopefully no one minds that I post a couple questions in a row as long as I'm following the rules:
1. Homework Statement
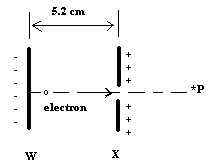
Two infinite parallel plates labelled W and X are separated by 5.2 cm. The electric potential between the plates is 150 V. An electron starts from rest at time tW and reaches plate X at time tX. The electron continues through the opening and reaches point P at time tP
c.) Find the electron’s kinetic energy and potential energy at point *P.
d.) Find the minimum speed of the electron at time tw needed for it to escape to infinity.
U = qV , energy conserved
We can calc. the KE X easily: Ux = 0, Ex = Uw, Uw = 150V * -1.60*10^-19 C = 1/2 m(e) v^2 so we have v and there is no electric field once it is outside of the plates. A previous given answer indicates that the speed is constant once we hit X (I don't understand why other than that no outside forces are acting on the electron if we exclude gravity), so how can we calculate U and K at *P?
1. Homework Statement
Two infinite parallel plates labelled W and X are separated by 5.2 cm. The electric potential between the plates is 150 V. An electron starts from rest at time tW and reaches plate X at time tX. The electron continues through the opening and reaches point P at time tP
c.) Find the electron’s kinetic energy and potential energy at point *P.
d.) Find the minimum speed of the electron at time tw needed for it to escape to infinity.
Homework Equations
U = qV , energy conserved
The Attempt at a Solution
We can calc. the KE X easily: Ux = 0, Ex = Uw, Uw = 150V * -1.60*10^-19 C = 1/2 m(e) v^2 so we have v and there is no electric field once it is outside of the plates. A previous given answer indicates that the speed is constant once we hit X (I don't understand why other than that no outside forces are acting on the electron if we exclude gravity), so how can we calculate U and K at *P?